题目内容
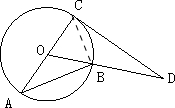
9、如图，AC为⊙O的直径，AB为⊙O的弦，∠A=35°，过点C的切线与OB的延长线相交于点D，则∠D=（ ）分析：连接BC，则∠ABC=90°，且∠A=35°，∠OCB=55°，又△BCO为等腰三角形，即有∠COB=70°，即可求∠D=90°-∠COB=20°．
解答：解：连接BC，
∴∠OCD=90°，
∴∠OCB=55°，
在△OCB中，OB=OC；
即有∠COB=70°；
∴∠D=90°-∠COB=20°．
故选A；
∴∠OCD=90°，
∴∠OCB=55°，
在△OCB中，OB=OC；
即有∠COB=70°；
∴∠D=90°-∠COB=20°．
故选A；
点评：本题利用了切线的概念和性质的应用以及三角形内角和为180°的知识点；在直角三角形中，同角或等角的余角相等；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
探索函数