题目内容
20.已知m、n是方程x2+2$\sqrt{2}$x+1=0的两根,则代数式$\sqrt{{m}^{2}+{n}^{2}+3mn}$值为3.分析 根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系得到m+n=-2$\sqrt{2}$,mn=1,再变形$\sqrt{{m}^{2}+{n}^{2}+3mn}$得$\sqrt{(m+n)^{2}+mn}$,然后把m+n=-2$\sqrt{2}$,mn=1整体代入计算即可.
解答 解:∵m、n是方程x2+2$\sqrt{2}$x+1=0的两根,
∴m+n=-2$\sqrt{2}$,mn=1,
∴$\sqrt{{m}^{2}+{n}^{2}+3mn}$=$\sqrt{(m+n)^{2}+mn}$=$\sqrt{(-2\sqrt{2})^{2}+1}$=3.
故答案为:3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两根分别为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了二次根式的化简求值.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
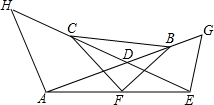 如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.