题目内容
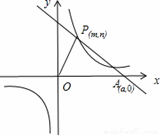
【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y = ![]() (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m). 设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m). 设△OPA的面积为s,且s=1+![]() .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值.
【答案】(1)a=![]() ; (2)k=2
; (2)k=2
【解析】试题分析:(1)根据三角形的面积公式得到s=![]() an.而s=1+
an.而s=1+![]() ,把n=1代入就可以得到a的值.
,把n=1代入就可以得到a的值.
(2)易证△OPA是等腰直角三角形,得到m=n=![]() ,根据三角形的面积S=
,根据三角形的面积S=![]() an,就可以解得k的值.
an,就可以解得k的值.
试题解析:解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m.
(1)当n=1时,s=![]() ,∴a=
,∴a=![]() =
=![]() .
.
(2)∵OP=AP,PA⊥OP,∴△OPA是等腰直角三角形,∴m=n=![]() ,∴1+
,∴1+![]() =
=![]() an.
an.
即n4﹣4n2+4=0,∴k2﹣4k+4=0,∴k=2.


练习册系列答案
相关题目