��Ŀ����
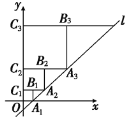
����Ŀ������������10�֣���ͼ��ֱ��y=��![]() x+6�ֱ���x�ᡢy�ύ��A��B���㣻ֱ��y=
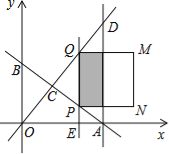
x+6�ֱ���x�ᡢy�ύ��A��B���㣻ֱ��y=![]() x��AB���ڵ�C�������A��ƽ����y���ֱ�߽��ڵ�D����E�ӵ�A��������ÿ��1����λ���ٶ���x�������˶�������E��x��Ĵ��ߣ��ֱ�ֱ��AB��OD��P��Q���㣬��PQΪ��������������PQMN����������PQMN����ACD�ص����֣���Ӱ���֣������ΪS��ƽ����λ������E���˶�ʱ��Ϊt���룩��
x��AB���ڵ�C�������A��ƽ����y���ֱ�߽��ڵ�D����E�ӵ�A��������ÿ��1����λ���ٶ���x�������˶�������E��x��Ĵ��ߣ��ֱ�ֱ��AB��OD��P��Q���㣬��PQΪ��������������PQMN����������PQMN����ACD�ص����֣���Ӱ���֣������ΪS��ƽ����λ������E���˶�ʱ��Ϊt���룩��
��1�����C�����꣮
��2����0��t��5ʱ����S��t֮��ĺ�����ϵʽ������S�����ֵ��
��3����t��0ʱ��ֱ��д���㣨5��3����������PQMN�ڲ�ʱt��ȡֵ��Χ��
���𰸡���1��C��3��![]() ������2��S=4t2��40t+100��S���=
������2��S=4t2��40t+100��S���=![]() ����3��3��t��4 �� t��7
����3��3��t��4 �� t��7
�������������������1����y=��![]() x+6��y=
x+6��y=![]() x�����ķ����鼴�ɣ�
x�����ķ����鼴�ɣ�
��2���ֱ����0��t��![]() ʱ��
ʱ��![]() ��t��5ʱ��S��t֮��ĺ�����ϵʽ��Ȼ�����ö��κ���������������ֵ���Ƚ�ȡ��ģ���3���㣨5��3����������PQMN�ڲ�ʱ����E��x�����˶�����������ۣ�
��t��5ʱ��S��t֮��ĺ�����ϵʽ��Ȼ�����ö��κ���������������ֵ���Ƚ�ȡ��ģ���3���㣨5��3����������PQMN�ڲ�ʱ����E��x�����˶�����������ۣ�
�����������1����ֱ��y=��![]() x+6��ֱ��y=
x+6��ֱ��y=![]() x���ڵ�C��
x���ڵ�C��
��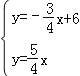 �����
�����![]() ��
��
��C��3��![]() ����
����
��2����A��������8��0����
�������⣬��AE=t��OE=8��t
����Q��������Ϊ![]() ��8��t������P��������Ϊ
��8��t������P��������Ϊ![]() t��
t��
��PQ=![]() ��8��t����
��8��t����![]() t=10��2t��
t=10��2t��
��0��t��![]() ʱ��S=t��10��2t������S=��2t2+10t����t=
ʱ��S=t��10��2t������S=��2t2+10t����t=![]() ʱ��S���=
ʱ��S���=![]()
��![]() ��t��5ʱ��S=��10��2t��2����S=4t2��40t+100����t=
��t��5ʱ��S=��10��2t��2����S=4t2��40t+100����t=![]() ʱ��S���=
ʱ��S���=![]()
��![]() ��
��![]() �� ��S���=
�� ��S���=![]()
��3��3��t��4 �� t��7

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�