题目内容
如图所示，CA为⊙O的切线，切点为A，点B在⊙O上，如果∠CAB=55°，那么∠AOB等于
- A.120°
- B.110°
- C.90°
- D.55°
B
分析：根据切线性质即可得出．
解答：根据切线的性质定理得∠OAC=90°，
则∠OAB=35°，
∴∠AOB=180°-35°×2=110°．
故选B．
点评：此题综合运用了切线的性质定理以及等边对等角的性质和三角形的内角和定理．
分析：根据切线性质即可得出．
解答：根据切线的性质定理得∠OAC=90°，
则∠OAB=35°，
∴∠AOB=180°-35°×2=110°．
故选B．
点评：此题综合运用了切线的性质定理以及等边对等角的性质和三角形的内角和定理．
练习册系列答案
相关题目
4、如图所示，CA为⊙O的切线，切点为A，点B在⊙O上，如果∠CAB=55°，那么∠AOB等于（ ）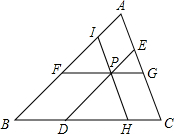
如图所示．P为△ABC内一点，过P点作线段DE，FG，HI分别平行于AB，BC和CA，且DE=FG=HI=d，AB=510，BC=450，CA=425．求d．
