题目内容
13.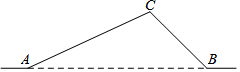 如图,从A地到B地的公路需经过C地,图中AC=50km,∠CAB=25°,∠CBA=45°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=50km,∠CAB=25°,∠CBA=45°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.(Ⅰ)求改直的公路AB的长;
(Ⅱ)问公路改直后比原来缩短了多少km?(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,$\sqrt{2}$取1.414)(结果保留小数点后一位)
分析 (1)过点C作CD⊥AB与D,根据AC=50千米,∠CAB=25°,求出CD、AD,根据∠CBA=45°,求出BD、BC,最后根据AB=AD+BD列式计算即可,
(2)根据AC和BC的长度,即可得出公路改直后该段路程比原来缩短的路程.
解答 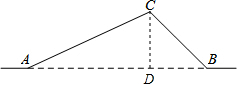 解:(1)过点C作CD⊥AB与D,
解:(1)过点C作CD⊥AB与D,
∵AC=50千米,∠CAB=25°,
∴CD=sin∠CAB•AC=sin25°×50≈0.42×50=21(千米),
AD=cos∠CAB•AC=cos25°×50≈0.91×50=45.5(千米),
∵∠CBA=45°,
∴BD=CD=21(千米),
BC=$\frac{CD}{sin∠CBA}$=$\frac{21}{sin45°}$≈29.7(千米),
∴AB=AD+BD=45.5+29.7=75.2(千米),
(2)∵AC=50千米,BC=29.7千米,
∴公路改直后该段路程比原来缩短50+29.7-76.7=3千米.
点评 此题主要考查了解直角三角形的应用,熟练掌握解直角三角形的方法是解题关键.

练习册系列答案
相关题目
18.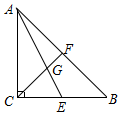 如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
 如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
5.甲、乙两名运动员每人射击10次,平均成绩为9环,要从中选一位发挥稳定的运动员参加市里比赛,则需关注的统计量是( )
| A. | 众数 | B. | 方差 | C. | 中位数 | D. | 平均数 |
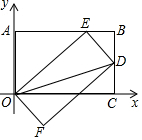 将矩形OABC如图放置在平面直角坐标系中,若OA=6,AB=10,点D为BC上一点,将矩形OABC沿OD折叠使得点C恰好落在AB边上的点E处.
将矩形OABC如图放置在平面直角坐标系中,若OA=6,AB=10,点D为BC上一点,将矩形OABC沿OD折叠使得点C恰好落在AB边上的点E处.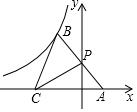 如图,双曲线y=$\frac{k}{x}$经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是-$\frac{16}{3}$.
如图,双曲线y=$\frac{k}{x}$经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是-$\frac{16}{3}$.