题目内容
 如图,在锐角△ABC中,高CD、BE相交于点H,则图中所有与△CEH相似(除△CEH自身外)的三角形的个数是
如图,在锐角△ABC中,高CD、BE相交于点H,则图中所有与△CEH相似(除△CEH自身外)的三角形的个数是
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:由在锐角△ABC中,高CD、BE相交于点H,即可得∠BDH=∠CEH=90°,又由对顶角相等,根据有两角对应相等的三角形相似,即可证得△BHD∽△CHE,同理可证得:△ADC∽△HEC,△ABE∽△HBD,即可求得答案.
解答:∵在锐角△ABC中,高CD、BE相交于点H,
∴∠BDH=∠CEH=90°,
∵∠BHD=∠CHE,
∴△BHD∽△CHE.
∵∠ADC=∠HEC=90°,∠ACD=∠HCE,
∴△ADC∽△HEC,
同理:△ABE∽△HBD,
∴△CEH∽△BDH∽△CDA∽△BEA.
∴与△CEH相似(除△CEH自身外)的三角形的个数是3个.
故选C.
点评:此题考查了相似三角形的判定.解题的关键是数形结合思想的应用与有两角对应相等的三角形相似定理的应用.
分析:由在锐角△ABC中,高CD、BE相交于点H,即可得∠BDH=∠CEH=90°,又由对顶角相等,根据有两角对应相等的三角形相似,即可证得△BHD∽△CHE,同理可证得:△ADC∽△HEC,△ABE∽△HBD,即可求得答案.
解答:∵在锐角△ABC中,高CD、BE相交于点H,
∴∠BDH=∠CEH=90°,
∵∠BHD=∠CHE,
∴△BHD∽△CHE.
∵∠ADC=∠HEC=90°,∠ACD=∠HCE,
∴△ADC∽△HEC,
同理:△ABE∽△HBD,
∴△CEH∽△BDH∽△CDA∽△BEA.
∴与△CEH相似(除△CEH自身外)的三角形的个数是3个.
故选C.
点评:此题考查了相似三角形的判定.解题的关键是数形结合思想的应用与有两角对应相等的三角形相似定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答: 25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.
25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.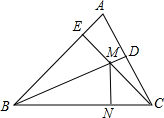 如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=
如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=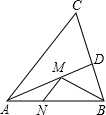 如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是
如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是