题目内容
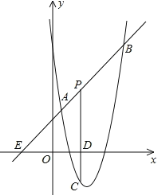
【题目】如图，已知抛物线y＝x2＋bx＋c经过矩形ABCD的两个顶点A、B，AB平行于x轴，对角线BD与抛物线交于点P，点A的坐标为(0，2)，AB＝4．
(1)求抛物线的解析式；
(2)若S△APO＝
，求矩形ABCD的面积．
【答案】（1）y=x2-4x+4（2）24
【解析】
（1）已知了A点坐标和AB的长，即可得出B点坐标，然后将A、B两点的坐标代入抛物线中，即可求出抛物线的解析式．
（2）根据三角形APO的面积可求出P点的横坐标，将其代入抛物线的解析式中即可求得P点的坐标．过P作PE⊥OA于E，通过构建的相似三角形DPE和DBA，可求出AD的长，有了长和宽即可求出矩形的面积．（也可通过求直线BP的解析式得出D点坐标来求出AD的长）
（1）由题意得，B点坐标为（4，2）
将点A（0，2），B（4，2）代入二次函数解析式得：
，
解得：
，
∴抛物线的解析式为y＝x24x＋2；
（2）由S△APO＝
可得：
OA|xp|＝，即×2×|xp|＝，
∴xp＝（负舍）
将xp＝代入抛物线解析式得：yP＝
，
过P点作垂直于y轴的垂线，垂足为E，
∵△DEP∽△DAB，
∴
，
解得：AD＝6，
∴S矩形ABCD＝24．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
