Question

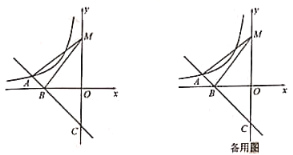
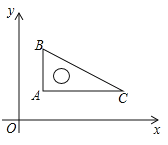
【题目】如图，在平面直角坐标系中，直角三角板∠C=30°，AB=4，将直角顶点放在点（，1）处，AC∥x轴，求经过点C的反比例函数的解析式．

Answer 1

【答案】．

【解析】试题分析：作AD⊥x轴交于点D，CE⊥x轴交于点E，要求经过点C的反比例函数的解析式，即要求出点C的坐标，点A的坐标已知，点C的纵坐标与点A的纵坐标相等，点C的横坐标为线段OE的长度，OD的长度与点A的横坐标相等，DE的长度可通过AB的长度以及tan30°求得.

试题解析：

作AD⊥x轴交于点D，CE⊥x轴交于点E，

∵A（，1），∴AD=，OD=1，

∴CE=AD=，

∵∠C=30°，AB=4，

∴AC==4，

∴ED=4，

∴EO=4+=5，

∴C（5，1），

设点C所在反比例函数解析式为y=，

则k=5，

∴反比例函数解析式为y=.