题目内容
若直线y=x+k与直线y=-
x+2的交点在y轴右侧,则k的取值范围是
| 1 | 2 |
k<2
k<2
.分析:根据两直线相交的问题解方程组
即可得到两直线的交点坐标为(
,
),然后根据题意得
>0,再解不等式即可.
|
| 4-2k |
| 3 |
| k+4 |
| 3 |
| 4-2k |
| 3 |
解答:解:解方程组
得
,
即两直线的交点坐标为(
,
),
∵直线y=x+k与直线y=-
x+2的交点在y轴右侧,
∴
>0,
∴k<2.
故答案为k<2.
|
|
即两直线的交点坐标为(
| 4-2k |
| 3 |
| k+4 |
| 3 |
∵直线y=x+k与直线y=-
| 1 |
| 2 |
∴
| 4-2k |
| 3 |
∴k<2.
故答案为k<2.
点评:本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
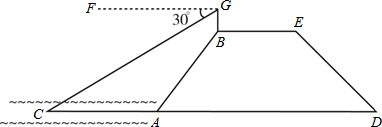


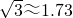 ,结果保留一位小数)
,结果保留一位小数)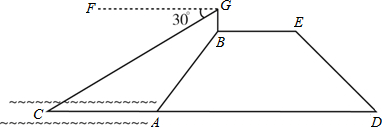
 ,结果保留一位小数)
,结果保留一位小数)