题目内容
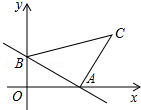 如图,一次函数y=-
如图,一次函数y=-| 2 | 3 |
(1)点A的坐标是(
3
3
,0
0
),点B的坐标是(0
0
,2
2
)(2)求Rt△ABC的面积.
(3)求过B、C两点直线的解析式.
分析:(1)根据坐标轴上的点的坐标特征,结合一次函数的解析式求出A、B两点的坐标;
(2)根据(1)中所求得出AO,BO的长,即可得出AB的长,再利用等腰直角三角形的性质得出Rt△ABC的面积;
(3)作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,AD=OB,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
(2)根据(1)中所求得出AO,BO的长,即可得出AB的长,再利用等腰直角三角形的性质得出Rt△ABC的面积;
(3)作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,AD=OB,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
解答:解:(1)一次函数y=-
x+2中,
令y=0,解得x=3.
则点A的坐标是(3,0).
令x=0得y=2.
则点B的坐标是(0,2);
故答案为:3,0,0,2;
(2)∵点A的坐标是(3,0),点B的坐标是(0,2),
∴BO=2,AO=3,
∴AB=
=
,
∵以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,
∴AC=AB=
,
∴Rt△ABC的面积为:
×
×
=
;
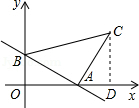 (3)如图所示:作CD⊥x轴于点D.
(3)如图所示:作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
在△ABO与△CAD中,
,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,
∴OD=OA+AD=5.
则点C的坐标是(5,3).
设直线BC的解析式是y=kx+b,
根据题意得:
,
解得:
.
则直线BC的解析式是:y=
x+2.
| 2 |
| 3 |
令y=0,解得x=3.
则点A的坐标是(3,0).
令x=0得y=2.
则点B的坐标是(0,2);
故答案为:3,0,0,2;
(2)∵点A的坐标是(3,0),点B的坐标是(0,2),
∴BO=2,AO=3,
∴AB=
| 22+32 |
| 13 |
∵以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,
∴AC=AB=
| 13 |
∴Rt△ABC的面积为:
| 1 |
| 2 |
| 13 |
| 13 |
| 13 |
| 2 |
 (3)如图所示:作CD⊥x轴于点D.
(3)如图所示:作CD⊥x轴于点D.∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
在△ABO与△CAD中,
|
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,
∴OD=OA+AD=5.
则点C的坐标是(5,3).
设直线BC的解析式是y=kx+b,
根据题意得:
|
解得:
|
则直线BC的解析式是:y=
| 1 |
| 5 |
点评:本题考查的是一次函数综合题,涉及到用待定系数法求一次函数的解析式、全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数