��Ŀ����
����Ŀ��ij���˱��ݻ���Ʒר��ƻ��ڴ���ǰϦ�����ס��������Ʒ�������г����У���������������Ϣ��
��Ϣһ�����ۼ��Ʒ��������y��Ԫ����������x������֮����ڶ��κ�����ϵy=ax2+bx����x=10ʱ��y=140����x=30ʱ��y=360��
��Ϣ���������ҿ��Ʒ��������y��Ԫ����������x������֮�����������������ϵy=3x�������������Ϣ������������⣻
��1������Ϣһ�ж��κ����ı���ʽ��
��2�������˱��ݻ���Ʒר��ƻ��ڴ���ǰϦ�����ס��������Ʒ��100���������һ��Ӫ��������ʹ���ۼס��������Ʒ��õ�����֮���������������
���𰸡���1��y=-0.1x2+15x����2�������ײ�Ʒ60���������Ҳ�Ʒ40�������������660Ԫ
�������������������1�����������ݴ�����κ�������ʽ��Ȼ�����ô���ϵ������⼴�ɣ�
��2���蹺���ײ�Ʒm�������Ҳ�Ʒ��10-m���������ۼס������ֲ�Ʒ��õ�����֮��ΪWԪ������������������ֲ�Ʒ������ĺ�����ʽ�����õ�W��m�ĺ�����ϵʽ���ٸ��ݶ��κ�������ֵ������
����������⣺��1������x=10ʱ��y=140����x=30ʱ��y=360��
��![]() ����ã�a=��0.1��b=15��
����ã�a=��0.1��b=15��
�����κ�������ʽΪy=��0.1x2+15x��
��2���蹺���ײ�Ʒm�������Ҳ�Ʒ��100-m���������ۼס������ֲ�Ʒ��õ�����֮��ΪWԪ����W=��0.1m2+15m+3��100-m��=��0.1m2+12m+300=��0.1��m-60��2+660��
��-0.1��0������m=60ʱ��W�����ֵ660Ԫ��
�𣺹����ײ�Ʒ60�����Ҳ�Ʒ40������ʹ���ۼס������ֲ�Ʒ��õ�����֮��������������660Ԫ��

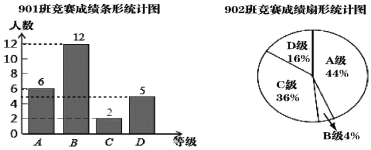
����Ŀ����ѧУ��֯����ѧϰǿ�����Ķ�֪ʶ�����У���901���902��������μӱ�����������ͬ���ɼ���ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֣�90�֣�80�ֺ�70�֣��꼶�鳤����ʦ��901���902��ijɼ��������������Ƴ����µ�ͳ��ͼ��
ƽ�������֣� | ��λ�����֣� | �������֣� | B������������ | |
901�� | 87.6 | 90 | 18 | |
902�� | 87.6 | 100 |
��1���ڱ��ξ����У�902��C�������ϵ������ж��٣�
��2�����㽫����������