题目内容
已知:A=ax2+x﹣1,B=3x2﹣2x+1(a为常数)
①若A与B的和中不含x2项,则a= ;
②在①的基础上化简:B﹣2A.
【考点】多项式.
【分析】①不含x2项,即x2项的系数为0,依此求得a的值;
②先将表示A与B的式子代入B﹣2A,再去括号合并同类项.
【解答】解:①A+B=ax2+x﹣1+3x2﹣2x+1=(a+3)x2﹣x
∵A与B的和中不含x2项,
∴a+3=0,解得a=﹣3.
②B﹣2A=3x2﹣2x+1﹣2×(﹣3x2+x﹣1)=3x2﹣2x+1+6x2﹣2x+2=9x2﹣4x+3.
【点评】多项式的加减实际上就是去括号和合并同类项.
多项式加减的运算法则:一般地,几个多项式相加减,如果有括号就先去括号,然后再合并同类项.
合并同类项的法则:把系数相加减,字母及字母的指数不变.
本题注意不含x2项,即x2项的系数为0.

练习册系列答案
相关题目


 ﹣
﹣ +
+ ﹣
﹣ )×(﹣36)
)×(﹣36)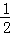 ∠ .
∠ .