题目内容
阅读下列材料:求函数y=
的最大值.
解:将原函数转化成x的一元二次方程,得(y-3)x2+(y-2)x+
y=0.
∵x为实数,∴△=(y-2)2-4(y-3)×
y=-y+4≥0,∴y≤4.因此,y的最大值为4.
根据材料给你的启示,求函数y=
的最小值.
| 3x2+2x |
| x2+x+0.25 |
解:将原函数转化成x的一元二次方程,得(y-3)x2+(y-2)x+
| 1 |
| 4 |
∵x为实数,∴△=(y-2)2-4(y-3)×
| 1 |
| 4 |
根据材料给你的启示,求函数y=
| 3x2+x+2 |
| x2+2x+1 |
分析:根据材料内容,可将原函数转换为(y-3)x2+(2y-1)x+y-2=0,继而根据△≥0,可得出y的最小值.
解答:解:将原函数转化成x的一元二次方程,得(y-3)x2+(2y-1)x+y-2=0,
∵x为实数,
∴△=(2y-1)2-4(y-3)(y-2)=16y-23≥0,
∴y≥
,
因此y的最小值为
.
∵x为实数,
∴△=(2y-1)2-4(y-3)(y-2)=16y-23≥0,
∴y≥
| 23 |
| 16 |
因此y的最小值为
| 23 |
| 16 |
点评:本题考查了一元二次方程的应用,这样的信息题,一定要熟读材料,套用材料的解题模式进行解答.

练习册系列答案
相关题目
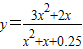 的最大值.
的最大值.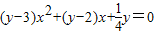 .
.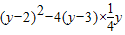 =-y+4≥0,∴y≤4.因此,y的最大值为4.
=-y+4≥0,∴y≤4.因此,y的最大值为4.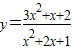 的最小值.
的最小值.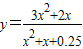 的最大值.
的最大值.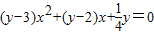 .
.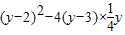 =-y+4≥0,∴y≤4.因此,y的最大值为4.
=-y+4≥0,∴y≤4.因此,y的最大值为4. 的最小值.
的最小值.