题目内容
梯形ABCD各边的中点分别是E、F、G、H，四边形EFGH是________．
平行四边形
分析：三角形的中位线平行于第三边，且等于第三边的一半．需注意新四边形的形状只与对角线有关，不用考虑原四边形的形状．
解答：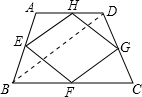
解：连接BD，
在△ABD中，E、H是AB、AD中点，
所以EH∥BD，EH=
BD；
在△BCD中，G、F是DC、BC中点，
所以GF∥BD，GF=BD，
所以EH=GF，EH∥GF，
所以四边形EFGH为平行四边形．
故答案为：平行四边形．
点评：本题考查了三角形的中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半．需注意新四边形的形状只与对角线有关，不用考虑原四边形的形状．
分析：三角形的中位线平行于第三边，且等于第三边的一半．需注意新四边形的形状只与对角线有关，不用考虑原四边形的形状．
解答：
解：连接BD，在△ABD中，E、H是AB、AD中点，
所以EH∥BD，EH=
BD；在△BCD中，G、F是DC、BC中点，
所以GF∥BD，GF=
BD，所以EH=GF，EH∥GF，
所以四边形EFGH为平行四边形．
故答案为：平行四边形．
点评：本题考查了三角形的中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半．需注意新四边形的形状只与对角线有关，不用考虑原四边形的形状．
练习册系列答案
相关题目
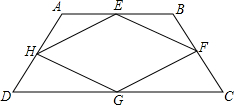、DA的中点．
16、如图，在四边形ABCD中，AC⊥BD，依次连接四边形ABCD各边的中点所得到的四边形为（ ）