Question

【题目】如图，在边长为的菱形中，对角线，点是直线上的动点，于，于．

如图，在边长为的菱形中，对角线，点是直线上的动点，于，于．

对角线的长是________，菱形的面积是________；

如图，当点在对角线上运动时，的值是否发生变化？请说明理由；

如图，当点在对角线的延长线上时，的值是否发生变化？若不变请说明理由，若变化，请直接写出、之间的数量关系，不用明理由．

Answer 1

【答案】624

【解析】

（1）连接AC与BD相交于点G，根据菱形的对角线互相垂直平分求出BG，再利用勾股定理列式求出AG，然后根据AC=2AG计算即可得解；再根据菱形的面积等于对角线乘积的一半列式计算即可得解；

（2）连接AO，根据S△ABD=S△ABO+S△ADO列式计算即可得解；

（3）连接AO，根据S△ABD=S△ABO-S△ADO列式整理即可得解．

解：（1）如图，连接AC与BD相交于点G，

在菱形ABCD中，AC⊥BD，BG=BD=×8=4，

由勾股定理得，AG=3，

∴AC=2AG=2×3=6，

菱形ABCD的面积=ACBD=×6×8=24；

故答案为：6；24；

（2）如图1，连接AO，

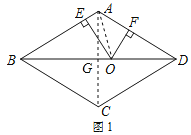
则S△ABD=S△ABO+S△ADO，

∴BDAG=ABOE+ADOF，

即×8×3=×5OE+×5OF，

解得OE+OF=4.8是定值，不变；

（3）如图2，连接AO，

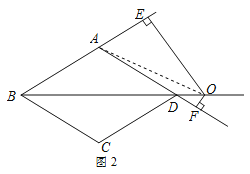
则S△ABD=S△ABO-S△ADO，

∴BDAG=ABOE-ADOF，

即×8×3=×5OE-×5OF，

解得OE-OF=4.8，是定值，不变，

∴OE+OF的值变化，OE、OF之间的数量关系为：OE-OF=4.8．