题目内容
【题目】如图，AB是⊙O的直径，TA切⊙O于点A，连结TB交⊙O于点C，∠BTA=40°，点M是圆上异于B，C的一个动点，则∠BMC的度数等于（ ）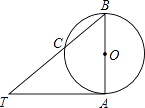
A.50°
B.50°或130°
C.40°
D.40°或140°
【答案】D
【解析】解：∵TA切⊙O于点A，
∴AT⊥AB，
∵∠BTA=40°，
∴∠B=90°﹣40°=50°，
∵OB=OC，
∴∠OCB=∠B=50°，
∴∠BOC=80°，
∵∠BMC= 
×80°=40°或∠BMC= ×（360﹣°80°）=140°．
所以答案是：D．
【考点精析】通过灵活运用三角形的内角和外角和圆内接四边形的性质，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题．
【题目】二次函数 
（a，b，c为常数，且 
）中的 
与 
的部分对应值如表：
| … | －1 | 0 | 1 | 3 | … |
| … | －1 | 3 | 5 | 3 | … |
下列结论：
① 
；
②当 
时，y的值随x值的增大而减小；
③3是方程 
的一个根；
④当 
时， 
．
其中正确的个数为（ ）
A.4个
B.3个
C.2个
D.1个
【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如下表（单位：秒）：
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | －3 | －4 | 4 | 2 | －2 | 2 | －1 | －1 | 2 |
乙种电子钟 | 4 | －3 | －1 | 2 | －2 | 1 | －2 | 2 | －2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数；
(2) 计算甲、乙两种电子钟走时误差的方差；
(3) 根据经验，走时稳定性较好的电子钟质量更优．若两种类型的电子钟价格相同，请问：你买哪种电子钟？为什么？
