题目内容
 如图,弧EF所在的⊙O的半径长为5,正三角形ABC的顶点A、B分别在半径OE、OF上,点C在弧EF上,∠EOF=60°,如果AB⊥OF,那么这个正三角形的边长为________.
如图,弧EF所在的⊙O的半径长为5,正三角形ABC的顶点A、B分别在半径OE、OF上,点C在弧EF上,∠EOF=60°,如果AB⊥OF,那么这个正三角形的边长为________.

分析:过C作CM⊥AB于M,连接OC,设正三角形ABC的边长是x,则MB=
 AB=
AB= x,由勾股定理求出CM=
x,由勾股定理求出CM= x,根据勾股定理求出OA2=25-x2,在Rt△ABO中,OA=
x,根据勾股定理求出OA2=25-x2,在Rt△ABO中,OA= =
= ,得出方程25-x2=
,得出方程25-x2= ,求出即可.
,求出即可.解答:

过C作CM⊥AB于M,连接OC,
设正三角形ABC的边长是x,
则MB=
 AB=
AB= x,∠BAC=60°,
x,∠BAC=60°,由勾股定理得:CM=
 x,
x,∵∠EOF=∠CAB=60°,AB⊥OF,
∴∠OAB=30°,∠OBA=90°,
∴OA2=OC2-AC2=25-x2,
在Rt△ABO中,OA=
 =
= ,
,OA2=
 ,
,25-x2=
 ,
,x=
 ,
,故答案为:
 .
.点评:本题考查了等边三角形性质,勾股定理,解直角三角形等知识点的应用,解此题的关键是能得出关于x的方程.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目


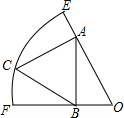 (2013•嘉定区一模)如图,弧EF所在的⊙O的半径长为5,正三角形ABC的顶点A、B分别在半径OE、OF上,点C在弧EF上,∠EOF=60°,如果AB⊥OF,那么这个正三角形的边长为
(2013•嘉定区一模)如图,弧EF所在的⊙O的半径长为5,正三角形ABC的顶点A、B分别在半径OE、OF上,点C在弧EF上,∠EOF=60°,如果AB⊥OF,那么这个正三角形的边长为 如图,在Rt△ABC中,∠B=90°,AB=1,BC=
如图,在Rt△ABC中,∠B=90°,AB=1,BC=