题目内容
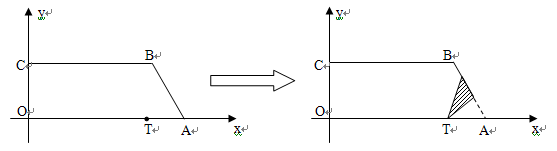
已知直角梯形纸片OABC在平面直角坐标系中的位置如图①所示，四
个顶点的坐标分别为O(0，0)，A(10，0)，B(8，2
)，C(0，2)，点P在线段OA上(不与O、A重合)，将纸片折叠，使点A落在射线AB上(记为点A’)，折痕PQ与射线AB交于点Q，设OP＝x，折叠后纸片重叠部分的面积为y．(图②供探索用)
1.求∠OAB的度数；
2.求y与x的函数关系式，并写出对应的x的取值范围；
3.y存在最大值吗？若存在，求出这个最大值，并求此时x的值；若不存在，说明理由．
【答案】
1.60°
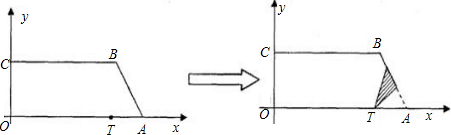
2.①当点A’在线段AB上时，y=
(10－x)2，……
6≤x＜10
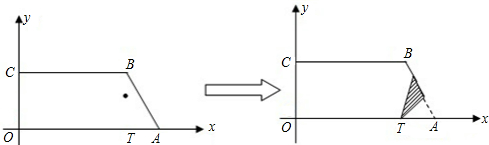
②当点A’在线段AB的延长线上，
y=－( x－2)2＋4
，……2＜x＜6
③当点A’和点Q都在线段AB的延长线上时，
y=
EF·OC=×4×2=4……0＜x≤2
3.y存在最大值
当6＜x＜10时，y=(10－x)2，
在对称轴x=10的左边，y的值随着x的增大而减小，
∴当x=6时，y的最大值是2
当2＜x＜6时，y=－(x－2)2+4
当x=2时，y的最大值是4，
当0＜x≤2时，y=4
综上所述，y的最大值是4，此时x的值是0＜x≤2
【解析】略
练习册系列答案
相关题目
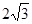)，C(0，