题目内容
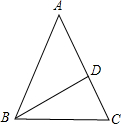 等腰三角形ABC的顶角A为36°,底角的平分线BD交AC于D,那么
等腰三角形ABC的顶角A为36°,底角的平分线BD交AC于D,那么| AD | AC |
分析:由题可知△ABC∽△BDC,然后根据相似比求解.
解答:解:∵等腰△ABC中,顶角∠A=36°,
∴∠ABC=72°,
又∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC=36°=∠A,
又∵∠C=∠C,
∴△ABC∽△BDC,
∴
=
,
设AD=x,AB=y,则BC=BD=AD=x,CD=y-x,
∴
=
,设
=k,则上式可以变化为
-1=k,
解得:k=
,则
的值等于
.
故答案为:
.
∴∠ABC=72°,
又∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC=36°=∠A,
又∵∠C=∠C,
∴△ABC∽△BDC,
∴
| CD |
| BC |
| BC |
| AB |
设AD=x,AB=y,则BC=BD=AD=x,CD=y-x,
∴
| y-x |
| x |
| x |
| y |
| x |
| y |
| 1 |
| k |
解得:k=
| ||
| 2 |
| AD |
| AC |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了黄金分割的知识,注意根据相似三角形的对应边的比,把问题转化为方程问题是关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
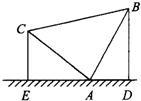 6、把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
6、把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( ) 把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为
把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为

 ;
;