题目内容
周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是
- A.S3>S4>S6
- B.S6>S4>S3
- C.S6>S3>S4
- D.S4>S6>S3
B
分析:先根据题意画出图形设出正六边形的边长,再根据正三角形、正方形、正六边形的周长都相等求出各图形的边长,再分别求出其面积即可.
解答: 解:设正六边形的边长为a,如图所示,
解:设正六边形的边长为a,如图所示,
则正△ABC的边长为2a,正方形ABCD的边长为 .
.
如图(1),过A作AD⊥BC,D为垂足;
∵△ABC是等边三角形,BC=2a,
∴BD=a,由勾股定理得,AD= =
=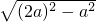 =
= a,
a,
∴S3=S△ABC= BC•AD=
BC•AD= ×2a×
×2a× a=
a= a2≈1.73a2.
a2≈1.73a2.
如图(2),∵四边形ABCD是正方形,
∴AB= ,
,
∴S4=S□ABCD=AB2= ×
× =
= a2≈2.25a2.
a2≈2.25a2.
如图(3),过O作OG⊥BC,G为垂足,
∵六边形ABCDEF是正六边形,
∴∠BOC= =60°,
=60°,
∴∠BOG=30°,OG= =
= =
= a.
a.
∴S△BOC= ×
× a×a=
a×a= a2,
a2,
∴S6=6S△BOC=6× a=
a= a2≈2.59a2.
a2≈2.59a2.
∵2.59a2>2.25a2>1.73a2.
∴S6>S4>S3.
故选:B.
点评:此题主要考查了正多边形和圆的性质,解答此题的关键是根据题意画出图形,再根据正三角形、正方形、正六边形的周长都相等设出其边长,求出其边长之间的关系,最后再分别求出其面积进行比较即可.
分析:先根据题意画出图形设出正六边形的边长,再根据正三角形、正方形、正六边形的周长都相等求出各图形的边长,再分别求出其面积即可.
解答:
 解:设正六边形的边长为a,如图所示,
解:设正六边形的边长为a,如图所示,则正△ABC的边长为2a,正方形ABCD的边长为
 .
.如图(1),过A作AD⊥BC,D为垂足;
∵△ABC是等边三角形,BC=2a,
∴BD=a,由勾股定理得,AD=
 =
=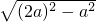 =
= a,
a,∴S3=S△ABC=
 BC•AD=
BC•AD= ×2a×
×2a× a=
a= a2≈1.73a2.
a2≈1.73a2.如图(2),∵四边形ABCD是正方形,
∴AB=
 ,
,∴S4=S□ABCD=AB2=
 ×
× =
= a2≈2.25a2.
a2≈2.25a2.如图(3),过O作OG⊥BC,G为垂足,
∵六边形ABCDEF是正六边形,
∴∠BOC=
 =60°,
=60°,∴∠BOG=30°,OG=
 =
= =
= a.
a.∴S△BOC=
 ×
× a×a=
a×a= a2,
a2,∴S6=6S△BOC=6×
 a=
a= a2≈2.59a2.
a2≈2.59a2.∵2.59a2>2.25a2>1.73a2.
∴S6>S4>S3.
故选:B.
点评:此题主要考查了正多边形和圆的性质,解答此题的关键是根据题意画出图形,再根据正三角形、正方形、正六边形的周长都相等设出其边长,求出其边长之间的关系,最后再分别求出其面积进行比较即可.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
周长相等的正三角形、正方形、正六边形、圆中,面积最大的是( )
| A、正三角形 | B、正方形 | C、正六边形 | D、圆 |