题目内容
在平面直角坐标系xOy中,直线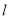 :
: 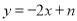 与抛物线
与抛物线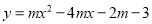 相交于点A(
相交于点A(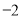 ,7).
,7).
(1)求m,n的值;
(2)过点A作AB∥x轴交抛物线于点B,设抛物线与x轴交于点C、D(点C在点D的左侧),求△BCD的面积;
(3)点E(t,0)为x轴上一个动点,过点E作平行于y轴的直线与直线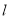 和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.
和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.
练习册系列答案
相关题目
题目内容
在平面直角坐标系xOy中,直线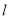 :
: 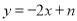 与抛物线
与抛物线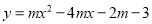 相交于点A(
相交于点A(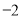 ,7).
,7).
(1)求m,n的值;
(2)过点A作AB∥x轴交抛物线于点B,设抛物线与x轴交于点C、D(点C在点D的左侧),求△BCD的面积;
(3)点E(t,0)为x轴上一个动点,过点E作平行于y轴的直线与直线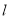 和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.
和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.