题目内容
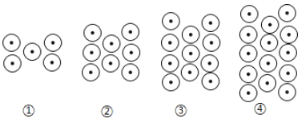
【题目】如图,都是由同样大小的⊙按一定规律所组成的,其中第一个图形有5个⊙,第二个图形一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第2019个图形中基本图形的个数为( )
A.6056B.6057C.6058D.6059
【答案】D
【解析】
将原图形中基本图形划分为中间部分和两边部分,中间基本图形个数等于序数,两边基本图形的个数和等于序数加1的两倍,据此规律可得答案.
解:∵第①个图形中基本图形的个数5=1+2×2,
第②个图形中基本图形的个数8=2+2×3,
第③个图形中基本图形的个数11=3+2×4,
第④个图形中基本图形的个数14=4+2×5,
…
∴第n个图形中基本图形的个数为n+2(n+1)=3n+2,
当n=2019时,3n+2=3×2019+2=6059,
故选:D.

【题目】按下列程序计算,把答案填写在表格里,然后看看有什么规律,想想为什么会有
这个规律?
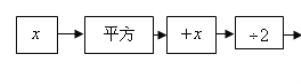
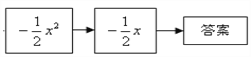
(1)填写表内空格:
输入 | 3 | 2 | -2 |
| … |
输出答案 | 0 | … |
(2)你发现的规律是____________.
(3)用简要过程说明你发现的规律的正确性.
【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)
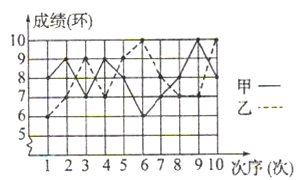
(1)依据折线统计图,得到下面的表格:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中![]() ________,
________,![]() ________;
________;
(2)甲成绩的众数是________环,乙成绩的中位数是________环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.