题目内容
 如图,已知∠AOB=60°,半径为2
如图,已知∠AOB=60°,半径为2| 3 |
| A、2 | B、2或6 |
| C、4或6 | D、1或5 |
考点:切线的性质
专题:计算题,压轴题
分析:讨论:当将⊙M水平向左平移,当点M运动到M′位置时,作MC⊥OA于C点,M′H⊥OA于H,M′Q⊥MC于Q,连结M′E,根据切线的性质得MM′∥OB,MC=2
,再根据垂径定理得EH=
EF=3,在Rt△EHM′中利用勾股定理计算出HM′=
,则CQ=M′H=
,所以MQ=2
-
=
,然后利用含30°的直角三角形三边的关系可得到MM′;
当将⊙M水平向左平移,当点M运动到M″位置时,作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,同理得到MC=2
,M′H=
,利用平行线的性质得∠MDC=∠M″DH=∠AOB=60°,则∠HM″D=30°,∠CMD=30°,根据含30°的直角三角形三边的关系可得到M″D和MD,则可得到MM″=6.
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
当将⊙M水平向左平移,当点M运动到M″位置时,作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,同理得到MC=2
| 3 |
| 3 |
解答: 解:当将⊙M水平向左平移,当点M运动到M′位置时,如图
解:当将⊙M水平向左平移,当点M运动到M′位置时,如图
作MC⊥OA于C点,M′H⊥OA于H,M′Q⊥MC于Q,连结M′E,
∵⊙M与边OB、OA相切,
∴MM′∥OB,MC=2
,
∵M′H⊥OA,
∴EH=CH=
EF=
×6=3,
在Rt△EHM′中,EM′=2
,
∴HM′=
=
,
∵M′Q⊥MC,
∴四边形M′QCH为矩形,
∴CQ=M′H=
,
∴MQ=2
-
=
,
∵∠QM′M=∠AOB=60°,
∴∠QM′M=30°,
∴M′Q=
=1,
∴MM′=2;
当将⊙M水平向左平移,当点M运动到M″位置时,如图2,
作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,
易得MC=2
,M′H=
,
∵∠MDC=∠M″DH=∠AOB=60°,
∴∠HM″D=30°,∠CMD=30°,
在Rt△HM″D中,M″D=
,则DH=
=1,
∴M″D=2DH=2,
在Rt△CDM中,CM=2
,则DC=
=2,
∴DM=2DC=4,
∴MM″=2+4=6,
综上所述,当⊙M平移的距离为2或6.
故选B.
 解:当将⊙M水平向左平移,当点M运动到M′位置时,如图
解:当将⊙M水平向左平移,当点M运动到M′位置时,如图作MC⊥OA于C点,M′H⊥OA于H,M′Q⊥MC于Q,连结M′E,
∵⊙M与边OB、OA相切,
∴MM′∥OB,MC=2
| 3 |
∵M′H⊥OA,
∴EH=CH=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△EHM′中,EM′=2
| 3 |
∴HM′=
| EM′2-EH2 |
| 3 |
∵M′Q⊥MC,
∴四边形M′QCH为矩形,
∴CQ=M′H=
| 3 |
∴MQ=2
| 3 |
| 3 |
| 3 |
∵∠QM′M=∠AOB=60°,
∴∠QM′M=30°,
∴M′Q=
| MQ | ||
|
∴MM′=2;
当将⊙M水平向左平移,当点M运动到M″位置时,如图2,
作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,
易得MC=2
| 3 |
| 3 |
∵∠MDC=∠M″DH=∠AOB=60°,
∴∠HM″D=30°,∠CMD=30°,
在Rt△HM″D中,M″D=
| 3 |
| M″D | ||
|
∴M″D=2DH=2,
在Rt△CDM中,CM=2
| 3 |
| MC | ||
|
∴DM=2DC=4,
∴MM″=2+4=6,
综上所述,当⊙M平移的距离为2或6.
故选B.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了垂径定理以及含30°的直角三角形三边的关系.

练习册系列答案
相关题目
要反映杭州市一天内气温的变化情况,比较适宜采用的是( )
| A、折线统计图 |
| B、条形统计图 |
| C、扇形统计图 |
| D、频数分布统计图 |
下列各图中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )
如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )| A、26cm2 |
| B、39cm2 |
| C、13cm2 |
| D、52cm2 |
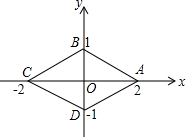 如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是
如图,菱形ABCD的顶点分别在x轴或y轴上,物体甲和物体乙分别由点A(2,0)同时出发,沿菱形ABCD的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以3个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是 小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.
小明利用测角仪测量学校内一棵大树的高度,已知他离树的水平距离BC为12m,测角仪的高度CD为1.4m,测到树顶A的仰角为50°,求树的高度AB.