题目内容
a,b,c均为不等于1的正数,且a-2=b3=c6,则abc的值为
- A.3
- B.2
- C.1
- D.

C
分析:先根据题意求出b=c2, =b3,然后求出a2b3=1,从而求出a2b3=a2b2b=a2b2c2=1,然后得出abc的值.
=b3,然后求出a2b3=1,从而求出a2b3=a2b2b=a2b2c2=1,然后得出abc的值.
解答:∵a-2=b3=c6,
∴b=c2, =b3,
=b3,
∴a2b3=1,
∴a2b3=a2b2b=a2b2c2=1,
∴abc=1.
故选C.
点评:本题主要考查了幂的乘方,积的乘方,理清指数的变化是解题的关键.
分析:先根据题意求出b=c2,
 =b3,然后求出a2b3=1,从而求出a2b3=a2b2b=a2b2c2=1,然后得出abc的值.
=b3,然后求出a2b3=1,从而求出a2b3=a2b2b=a2b2c2=1,然后得出abc的值.解答:∵a-2=b3=c6,
∴b=c2,
 =b3,
=b3,∴a2b3=1,
∴a2b3=a2b2b=a2b2c2=1,
∴abc=1.
故选C.
点评:本题主要考查了幂的乘方,积的乘方,理清指数的变化是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
a,b,c均为不等于1的正数,且a-2=b3=c6,则abc的值为( )
| A、3 | ||
| B、2 | ||
| C、1 | ||
D、
|
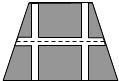 如图,要设计一个等腰梯形的花坛,花坛上底长12米,下底长18米,高8米.
如图,要设计一个等腰梯形的花坛,花坛上底长12米,下底长18米,高8米.