题目内容
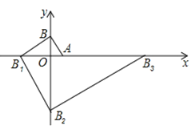
【题目】如图所示，把多块大小不同的
角三角板，摆放在平面直角坐标系中，第一块三角板
的一条直角边与
轴重合且点
的坐标为
，
，第二块三角板的斜边
与第一块三角板的斜边
垂直且交轴于点
，第三块三角板的斜边
与第二块三角板的斜边垂直且交
轴于点
，第四块三角板斜边
与第三块三角板的斜边垂直且交轴于点
，按此规律继续下去，则点
的坐标为（ ）
A.
B.
C.
D.
【答案】D
【解析】
计算出OB 、OB1、 OB2的长度，根据题意和图象可以发现题目中的变化规律，从而可以求得点B2018的坐标．
解：由题意可得，
OB = 
= 
，
OB1= 
OB= 
= 
，
OB2= OB1= 
，
…
∵2018÷4=504…2，
∴点B2018在y轴的负半轴上，
∴点B2018的坐标为
．
故答案为：D．
练习册系列答案
优学名师名题系列答案
相关题目
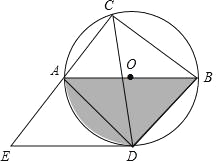
【题目】如图，⊙O的直径AB=12，弦AC=6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD．
（1）由AB，BD，
围成的阴影部分的面积是 ；
（2）求线段DE的长．
