Question

【题目】实践操作

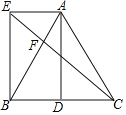
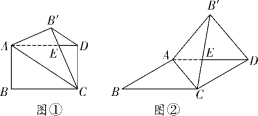
如图①，将矩形纸片沿对角线翻折，使点落在矩形所在平面内，和相交于点E，连接．

解决问题

（1）在图①中，

①和的位置关系为________；

②将剪下后展开，得到的图形是________；

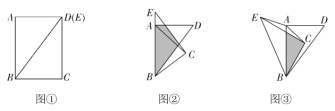
（2）若图①中的矩形变为平行四边形时（），如图②所示，结论①和结论②是否成立，若成立，请挑选其中的一个结论加以证明，若不成立，请说明理由；

拓展应用

（3）在图②中，若，当恰好为直角三角形时，求的长度．

Answer 1

【答案】（1）①，②菱形；（2）结论仍成立．证明见解析；（3）的长度为4或6或8或12．

【解析】

解：（1）①（平行）；

【解法提示】由折叠性质知，由矩形性质知，∴，∴，即，∴，又由题知，∴，即，∵，∴，∴．

②菱形；

【解法提示】由（1）①知，即是等腰三角形，∴剪开后得到四边相等的四边形即菱形．

（2）结论仍成立．

若选择结论①，证明：

由折叠性质知，

∵，

∴，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

∴；

若选择结论②，证明：

如图①，设点E的对应点为F，

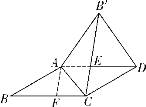
图①

∵四边形是平行四边形，

∴，

∴，

由折叠性质知，

∴，

∴，

∵，

∴，

∴四边形为平行四边形，

又∵，

∴四边形为菱形；

即将剪下后展开，得到的图形是菱形；

（3）解：情况1：如图②，当时，即．

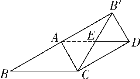
图②

同（1）①易知，

∴即，

由折叠性质知，

在中，，∴；

情况2：如图③，当时，

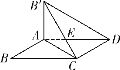
图③

由翻折性质知，

∴在中，，

则，

同（1）①易知和都是等腰三角形，

∴，

∴；

情况3：如图④，当时，即，

图④

由得，即，

在中，，

∴；

情况4：如图⑤，当时，

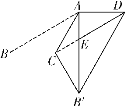
图⑤

由平行四边形性质得，

，

∴，

同（1）①易知和都是等腰三角形，

∴，

∴，

∵，

∴，

在中，，

∴．

综上所述，的长度为4或6或8或12．