Question

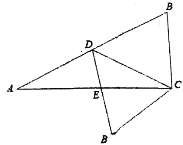
【题目】已知Rt△ABC，∠ACB=90，BC=10，AC=20，点D为斜边中点，连接CD，将△BCD沿CD翻折得△B’CD，B’D交AC于点E，则的值为（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

如图，过点B作BH⊥CD于H，过点E作EF⊥CD于F，由勾股定理可求AB的长，由锐角三角函数可求BH，CH，DH的长，由折叠的性质可得∠BDC=∠B'DC，S△BCD=S△DCB'=50，利用锐角三角函数可求EF=，由面积关系可求解．

解：如图，过点B作BH⊥CD于H，过点E作EF⊥CD于F，

∵∠ACB=90°，BC=10，AC=20，

∴AB=，S△ABC=×10×20=100，

∵点D为斜边中点，∠ACB=90°，

∴AD=CD=BD=，

∴∠DAC=∠DCA，∠DBC=∠DCB，

∴sin∠BCD=sin∠DBC=，

∴，

∴BH=，

∴CH=，

∴DH=，

∵将△BCD沿CD翻折得△B′CD，

∴∠BDC=∠B'DC，S△BCD=S△DCB'=50，

∴tan∠BDC=tan∠B'DC=，

∴，

∴设DF=3x，EF=4x，

∵tan∠DCA=tan∠DAC=，

∴，

∴FC=8x，

∵DF+CF=CD，

∴3x+8x=，

∴x=，

∴EF=，

∴S△DEC=×DC×EF=，

∴S△CEB'=50-=，

∴，

故选：A．