题目内容
如图1,D是△ABC的边BC上一点,AH⊥BC于H,S△ABD= BD•AH,S△ADC=
BD•AH,S△ADC= DC•AH,则
DC•AH,则 ,因此,利用三角形的面积比可以来表示两条线段的比,甚至用三角形面积的比来证明与线段比有关的命题.
,因此,利用三角形的面积比可以来表示两条线段的比,甚至用三角形面积的比来证明与线段比有关的命题.

请解决下列问题:
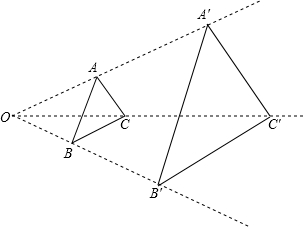
已知:如图2,直线l与△ABC的边AB、AC交于D、F,与BC的延长线交于E,连接BF、AE.
(1)求证: ;
;
(2)求证: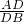 •
• •
• =1.
=1.
 证明:(1)过A、B分别作DE的垂线段AM、BN,如图.
证明:(1)过A、B分别作DE的垂线段AM、BN,如图.∵S△AEF=
 EF•AM,S△BEF=
EF•AM,S△BEF= EF•BN,
EF•BN,∴
 =
=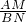 .
.∵在△ADM与△BDN中,
 ,
,∴△ADM∽△BDN,
∴
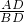 =
=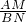 ,
,∴
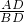 =
= ;
;(2)设F到BE的距离为h,则
 =
= =
= ,
,同理,得到
 =
= ,
,又由(1)得出
 =
=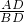 ,
,将这三个式子相乘,得
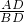 •
• •
• =
= •
• •
• =1.
=1.即
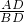 •
• •
• =1.
=1.分析:(1)过A、B分别作DE的垂线段AM、BN,根据同底的两个三角形面积之比等于高之比,得出
 =
=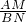 ,再证明△ADM∽△BDN,由相似三角形对应边成比例得出
,再证明△ADM∽△BDN,由相似三角形对应边成比例得出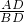 =
=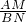 ,进而证明出
,进而证明出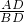 =
= ;
;(2)根据同高的两个三角形面积之比等于底之比,得出
 =
= ,
, =
= ,又由(1)得出
,又由(1)得出 =
=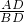 ,将这三个式子相乘,即可证明出结论.
,将这三个式子相乘,即可证明出结论.点评:本题考查了相似三角形的判定与性质,利用三角形的面积比表示两条线段的比,同时考查了学生的理解能力及知识的迁移能力,难度适中.(1)问分别作出△AEF与△BEF中EF边上的高是解题的关键.

练习册系列答案
相关题目
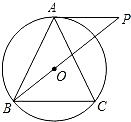 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
 (2012•利川市二模)如图,点P是△ABC三条角平分线的交点,若∠BPC=108°,则下列结论中正确的是( )
(2012•利川市二模)如图,点P是△ABC三条角平分线的交点,若∠BPC=108°,则下列结论中正确的是( ) 如图,点O是△ABC的内心,若∠BAC=86°,则∠BOC=( )
如图,点O是△ABC的内心,若∠BAC=86°,则∠BOC=( )