题目内容
如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG

解:∵ 四边形ABCD是正方形
∴ AB=BC=CD=DA
∠DAB=∠ABC=90°
 ∴ ∠DAE+∠GAB=90°
∴ ∠DAE+∠GAB=90°
∵ DE⊥AG BF⊥AG
∴ ∠AED=∠BFA=90°
∠DAE +∠ADE=90°
∴ ∠GAB =∠ADE
在△ABF和△DAE中

∴ △ABF≌△DAE
(2)作图略  方法1:作HI⊥BM于点I
方法1:作HI⊥BM于点I
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGI=90°
∵ HI⊥BM
∴ ∠GHI+∠HGI=90°
∴ ∠AGB =∠GHI
∵ G是BC中点
∴ tan∠AGB=
∴ tan∠GHI= tan∠AGB=
∴ GI=2HI
∵ CH平分∠DCM
∴ ∠HCI=
∴ CI=HI
∴ CI=CG=BG=HI
在△ABG和△GIH中

∴ △ABG≌△GIH
∴ AG=GH
 方法2: 作AB中点P,连结GP
方法2: 作AB中点P,连结GP
∵ P、G分别是AB、BC中点 且AB=BC
∴ AP=BP=BG=CG ∴ ∠BPG=45°
∵ CH平分∠DCM
∴ ∠HCM=
∴ ∠APG=∠HCG=135
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGM=90°
∵ ∠BAG+∠AGB=90°
∴ ∠BAG =∠HGM
在△AGP和△GHC中

∴ △AGP≌△GHC
∴ AG=GH

练习册系列答案
相关题目
 时,求图中阴影部分的面积。(结果保留2个有效数字,
时,求图中阴影部分的面积。(结果保留2个有效数字, ≈1.73,
≈1.73, ≈3.14).
≈3.14). 
 和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.(原创)
和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.(原创)



 ,∠C=60°,求
,∠C=60°,求 的长
的长
 x2 -
x2 -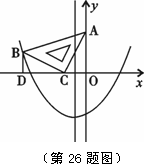 (3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.