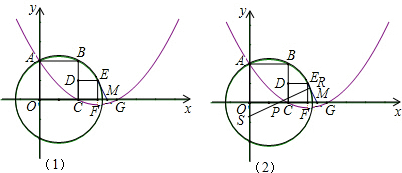题目内容
 (2013•盐城模拟)定义:如图,若双曲线y=
(2013•盐城模拟)定义:如图,若双曲线y=| k |
| x |
| k |
| x |
| k |
| x |
| 2 |
9
9
.分析:根据题中的新定义:可得出对径AB=OA+OB=2OA,由已知的对径长求出OA的长,过A作AM垂直于x轴,设A(a,a),a大于0,在直角三角形AOM中,利用勾股定理列出关于a的方程,求出方程的解得到a的值,确定出A的坐标,将A的坐标代入反比例解析式中,即可求出k的值.
解答: 解:过A作AM⊥x轴,交x轴于点M,如图所示:
解:过A作AM⊥x轴,交x轴于点M,如图所示:
设A(a,a),a>0,可得出AM=OM=a,
又∵双曲线的对径AB=6
,
∴OA=OB=3
,
在Rt△AOM中,根据勾股定理得:AM2+OM2=OA2,
则a2+a2=(3
)2,
解得:a=3或a=-3(舍去),
则A(3,3),
将x=3,y=3代入反比例解析式得:3=
,
解得:k=9.
故答案为:9
 解:过A作AM⊥x轴,交x轴于点M,如图所示:
解:过A作AM⊥x轴,交x轴于点M,如图所示:设A(a,a),a>0,可得出AM=OM=a,
又∵双曲线的对径AB=6
| 2 |
∴OA=OB=3
| 2 |
在Rt△AOM中,根据勾股定理得:AM2+OM2=OA2,
则a2+a2=(3
| 2 |
解得:a=3或a=-3(舍去),
则A(3,3),
将x=3,y=3代入反比例解析式得:3=
| k |
| 3 |
解得:k=9.
故答案为:9
点评:此题考查了反比例函数与一次函数的交点问题,属于新定义的题型,涉及的知识有:勾股定理,坐标与图形性质,以及待定系数法确定函数解析式,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 (2013•盐城模拟)如图所示,在建立平面直角坐标系后,△ABC顶点A的坐标为(1,-4),若以原点O为位似中心,在第二象限内画△ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的位似比等于
(2013•盐城模拟)如图所示,在建立平面直角坐标系后,△ABC顶点A的坐标为(1,-4),若以原点O为位似中心,在第二象限内画△ABC的位似图形△A′B′C′,使△A′B′C′与△ABC的位似比等于
 (2013•盐城模拟)已知四边形ABCD的外接圆⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,
(2013•盐城模拟)已知四边形ABCD的外接圆⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,