题目内容
Rt△ABC中，∠C=90°，直角边AC是直角边BC的3倍，则sinA的值是分析：根据题意画出图形，设BC=x，则AC=3x，由勾股定理可求出AB的长，再根据锐角三角函数的定义即可求出sinA的值．
解答：
解：根据题意画出图形，如图：
设BC=x，则AC=3x，由勾股定理得，AB=
=
=
x，
由锐角三角函数的定义得，sinA=
=
=
．
故答案为：
．
解：根据题意画出图形，如图：设BC=x，则AC=3x，由勾股定理得，AB=
| AC2+BC2 |
| (3x)2+x2 |
| 10 |
由锐角三角函数的定义得，sinA=
| BC |
| AB |
| x | ||
|
| ||
| 10 |
故答案为：
| ||
| 10 |
点评：本题考查的是锐角三角函数的定义及勾股定理，通过设参数的方法得出直角三角形各边的关系是解答此题的关键．
练习册系列答案
相关题目
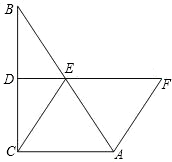延长线上，且AF=CE．求证：四边形ACEF是菱形．
如图，在Rt△ABC中，∠BAC=90°，点D、E、F分别是三边的中点，且CF=3cm，则DE=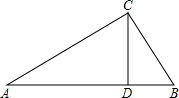
如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=
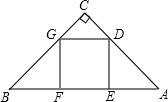点G在边BC上．
如图，Rt△ABC中，∠C=90°，D为AB的中点，DE⊥AB，AB=20，AC=12，则四边形ADEC的面积为