题目内容
 如图,在正方形ABCD中,AB=1,在边BC的延长线上取一点E,使CE=CA,AE与CD相交于点F.求:tan22.5°的值(结果用根号表示).
如图,在正方形ABCD中,AB=1,在边BC的延长线上取一点E,使CE=CA,AE与CD相交于点F.求:tan22.5°的值(结果用根号表示).
解:∵在正方形ABCD中,AB=1,
∴AC= ,
,
而CE=CA,
∴∠E=∠CAE,
∴BE=BC+CE= +1,
+1,
而∠ACB=45°
∴tan∠E=tan22.5°=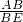 =
=
 -1.
-1.
分析:由于正方形ABCD中,AB=1,根据勾股定理可以求出线段AC的长度,也就求出线段CE的长度,再根据三角函数的定义即可求解.
点评:此题分别考查了相似三角形的性质与判定、正方形的性质及三角函数的定义,同时也利用勾股定理,有一定的综合性,要求学生熟练掌握相关知识才能解决问题.
∴AC=
 ,
,而CE=CA,
∴∠E=∠CAE,
∴BE=BC+CE=
 +1,
+1,而∠ACB=45°
∴tan∠E=tan22.5°=
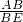 =
=
 -1.
-1.分析:由于正方形ABCD中,AB=1,根据勾股定理可以求出线段AC的长度,也就求出线段CE的长度,再根据三角函数的定义即可求解.
点评:此题分别考查了相似三角形的性质与判定、正方形的性质及三角函数的定义,同时也利用勾股定理,有一定的综合性,要求学生熟练掌握相关知识才能解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6