题目内容
已知:如图,⊙O中,直径AB=5,在它的不同侧有定点C和动点P,BC:CA=4:3,点P在 |
| AB |
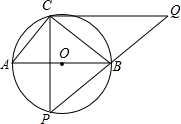 作CP的垂线,与PB的延长线交于点Q.
作CP的垂线,与PB的延长线交于点Q.(l)当点P与点C关于AB对称时,求CQ的长;
(2)当点P运动到
 |
| AB |
(3)当点P运动到
 |
| AB |
分析:(1)由题意得,∠ACB=90°,由勾股定理得BC,AC,即可得出CD,PC,则△ACB∽△PCQ,
=
,求得CQ;
(2)根据已知得BE,再由三角函数得出PE,PC,从而求出CQ;
(3)点P在
上运动时,有CQ=
PC.当PC最大时,CQ取到最大值,即可求得CQ最大值.
| AC |
| PC |
| BC |
| CQ |
(2)根据已知得BE,再由三角函数得出PE,PC,从而求出CQ;
(3)点P在
 |
| AB |
| 4 |
| 3 |
解答: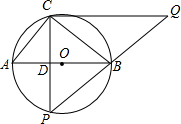 解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D,
解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D,
∵AB为⊙O的直径,
∴∠ACB=90°,(1分)
∵AB=5,BC:CA=4:3,
∴BC=4,AC=3,
∵AC•BC=AB•CD,
∴CD=
.(2分),
∴PC=
.
在Rt△ACB和Rt△PCQ中,
∠ACB=∠PCQ=90°,∠CAB=∠CPQ,
∴△ACB∽△PCQ,
∴
=
,
∴CQ=
PC=
;(3分)
(2)当点P运动到
的中点时,过点B作BE⊥PC于点E.
∵点P是
的中点,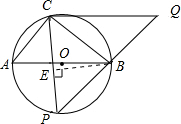
∴∠PCB=45°,
BE=CE=
BC=2
.(4分)
在Rt△EPB中,tan∠EPB=
=
∴PE=
BE=
.
∴PC=PE+CE=
.(5分).
∴CQ=
PC=
.(6分)
(3)点P在
上运动时,恒有CQ=
PC.
所以PC最大时,CQ取到最大值,
当PC过圆心O,即PC取最大值5时,CQ最大值为
.(7分)
 解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D,
解:(1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D,∵AB为⊙O的直径,
∴∠ACB=90°,(1分)
∵AB=5,BC:CA=4:3,
∴BC=4,AC=3,
∵AC•BC=AB•CD,
∴CD=
| 12 |
| 5 |
∴PC=
| 24 |
| 5 |
在Rt△ACB和Rt△PCQ中,
∠ACB=∠PCQ=90°,∠CAB=∠CPQ,
∴△ACB∽△PCQ,
∴
| AC |
| PC |
| BC |
| CQ |
∴CQ=
| 4 |
| 3 |
| 32 |
| 5 |
(2)当点P运动到
 |
| AB |
∵点P是
 |
| AB |

∴∠PCB=45°,
BE=CE=
| ||
| 2 |
| 2 |
在Rt△EPB中,tan∠EPB=
| BE |
| PE |
| 4 |
| 3 |
∴PE=
| 3 |
| 4 |
3
| ||
| 2 |
∴PC=PE+CE=
7
| ||
| 2 |
∴CQ=
| 4 |
| 3 |
14
| ||
| 3 |
(3)点P在
 |
| AB |
| 4 |
| 3 |
所以PC最大时,CQ取到最大值,
当PC过圆心O,即PC取最大值5时,CQ最大值为
| 20 |
| 3 |
点评:本题考查了相似三角形的判定和性质、圆周角定理和解直角三角形,是中考压轴题,难度偏大.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 30、已知:如图,△ABC中,AB=AC,∠1=∠2,
30、已知:如图,△ABC中,AB=AC,∠1=∠2, (2013•江宁区一模)已知:如图,△ABC中,以AB为直径的⊙O交AC于点D,且D为AC的中点,过D作DE丄CB,垂足为E.
(2013•江宁区一模)已知:如图,△ABC中,以AB为直径的⊙O交AC于点D,且D为AC的中点,过D作DE丄CB,垂足为E. (2012•丰润区一模)已知,如图,△ABC中,∠C>∠B.
(2012•丰润区一模)已知,如图,△ABC中,∠C>∠B. 已知:如图,△ABC中,BC边上有D、E两点,∠1=∠2,∠3=∠4.
已知:如图,△ABC中,BC边上有D、E两点,∠1=∠2,∠3=∠4. 已知:如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,且∠BDE=∠BED,∠A=100°,求∠DEC的度数.
已知:如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,且∠BDE=∠BED,∠A=100°,求∠DEC的度数.