题目内容
【题目】一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
含有两个字母![]() ,
, ![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
, ![]() 等对称式都可以用
等对称式都可以用![]() 和
和![]() 表示,例如:
表示,例如: ![]() .
.
请根据以上材料解决下列问题:
(![]() )式子①
)式子①![]() ,②
,②![]() ,③
,③![]() 中,属于对称式的是__________(填序号).
中,属于对称式的是__________(填序号).
(![]() )已知
)已知![]() .
.
①若![]() ,
, ![]() ,求对称式
,求对称式![]() 的值.
的值.
②若![]() ,直接写出对称式
,直接写出对称式![]() 的最小值.
的最小值.
【答案】(![]() )①③.(
)①③.(![]() )①
)①![]() .②
.②![]()
【解析】试题分析:(1)由对称式的定义对三个式子一一进行判断可得属于对称式的是①、③;(2)①将等号左边的式子展开, 由等号两边一次项系数和常数项对应相等可得a+b=m,ab=n,已知m、n的值,所以a+b、ab的值即求得,因为![]() +
+![]() =
=![]() =
=![]() ,所以将a+b、ab的值整体代入化简后的式子计算出结果即可;②
,所以将a+b、ab的值整体代入化简后的式子计算出结果即可;②![]() +
+![]() = a2+
= a2+![]() +b2+
+b2+![]() =(a+b)2-2ab
=(a+b)2-2ab![]() =m2+8+
=m2+8+![]() =
=![]() +
+![]() ,因为
,因为![]() m2≥0,所以
m2≥0,所以![]() m2+
m2+![]() ≥
≥![]() ,所以
,所以![]() +
+![]() 的最小值是
的最小值是![]() .
.
试题解析:
(![]() )∵a2b2=b2a2,∴a2b2是对称式,
)∵a2b2=b2a2,∴a2b2是对称式,
∵a2-b2≠b2-a2,∴a2-b2不是对称式,
∵![]() +
+![]() =
=![]() +
+![]() ,∴
,∴![]() +
+![]() 是对称式,
是对称式,
∴①、③是对称式;
(![]() )①∵(x+a)(x+b)=x2+(a+b)x+ab=x2+mx+n,
)①∵(x+a)(x+b)=x2+(a+b)x+ab=x2+mx+n,
∴a+b=m,ab=n,
∵m=-2![]() ,n=
,n=![]() ,
,
∴![]() +
+![]() =
=![]() =
=![]() =
=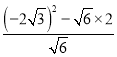 =
=![]() =2
=2![]() -2;
-2;
②![]() +
+![]() ,
,
=a2+![]() +b2+
+b2+![]() ,
,
=(a+b)2-2ab+![]() ,
,
=m2+8+![]() ,
,
=![]() +
+![]() ,
,
∵![]() m2≥0,
m2≥0,
∴![]() m2+
m2+![]() ≥
≥![]() ,
,
∴![]() +
+![]() 的最小值是
的最小值是![]() .
.

练习册系列答案
相关题目