题目内容
已知直线y=3x+4与抛物线y=x2相交于A、B两点(点B在y轴两侧),求:
(1)求A,B的坐标;
(2)求△ABO的面积;
(3)求一次函数值小于二次函数值的x的取值范围.
(1)求A,B的坐标;
(2)求△ABO的面积;
(3)求一次函数值小于二次函数值的x的取值范围.
考点:二次函数的性质,二次函数与不等式(组)
专题:
分析:(1)由直线y=-2x+3与抛物线y=x2相交联立方程,求得A、B两点坐标;
(2)由A、B两点向x轴作垂线,利用梯形及三角形面积计算方法即可求得△ABO的面积;
(3)根据函数的图象即可求得x的取值范围.
(2)由A、B两点向x轴作垂线,利用梯形及三角形面积计算方法即可求得△ABO的面积;
(3)根据函数的图象即可求得x的取值范围.
解答: 解:(1)如图,直线y=3x+4与抛物线y=x2相交,
解:(1)如图,直线y=3x+4与抛物线y=x2相交,
即x2=3x+4,
解得x1=4,x2=-1.
因此交点坐标为A为(4,16),B为(-1,1),
(2)作AA1,BB1分别垂直于x轴,垂足为A1,B1,
∴S△OAB=S梯形AA1B1B-S△AA1O-S△BB1O
=
×(1+16)×(1+4)-
×16×4-
×1×1
=10.
(3)由图象可知当x<-1或x>4时,一次函数值小于二次函数值.
 解:(1)如图,直线y=3x+4与抛物线y=x2相交,
解:(1)如图,直线y=3x+4与抛物线y=x2相交,即x2=3x+4,
解得x1=4,x2=-1.
因此交点坐标为A为(4,16),B为(-1,1),
(2)作AA1,BB1分别垂直于x轴,垂足为A1,B1,
∴S△OAB=S梯形AA1B1B-S△AA1O-S△BB1O
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=10.
(3)由图象可知当x<-1或x>4时,一次函数值小于二次函数值.
点评:此题考查一次函数与二次函数交点问题,以及梯形及三角形面积计算方法.

练习册系列答案
相关题目
计算(-1)2014+(-1)2015的结果为( )
| A、-4 029 | B、-2 |
| C、0 | D、2 |
用四舍五入法取1.4938精确到百分位的值是( )
| A、1.49 | B、1.490 |
| C、1.5 | D、1.50 |

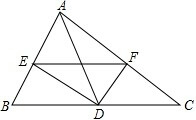 如图,在△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE、DF分别交AB、AC于E、F,且BE2+CF2=EF2,求证:△ABC为直角三角形.
如图,在△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE、DF分别交AB、AC于E、F,且BE2+CF2=EF2,求证:△ABC为直角三角形.