题目内容
9. 如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.(1)证明:DE为⊙O的切线;
(2)若BC=4,求AD的长.
分析 (1)连接OD,由平行线的判定定理可得OD∥AC,利用平行线的性质得∠ODE=∠DEA=90°,可得DE为⊙O的切线;
(2)连接CD,由BC为直径,利用圆周角定理可得∠ADC=90°,由∠A=30°,AC=BC=4,利用锐角三角函数可得AD.
解答 (1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠B,
∵AC=BC,
∴∠A=∠B,
∴∠ODB=∠A,
∴OD∥AC,
∴∠ODE=∠DEA=90°,
∴DE为⊙O的切线;
(2)解:连接CD,
∵BC为直径,
∴∠ADC=90°,
∵∠A=30°,
又∵AC=BC=4,
∴AD=AC•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
点评 本题主要考查了圆周角定理,平行线的性质及判定定理,作出恰当的辅助线构建直角三角形是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
17.下列各组中,两个单项式是同类项的是( )
| A. | 3mn与-4nm | B. | -mn2与m2n | C. | 2x3与-3y3 | D. | 3ab与-abc |
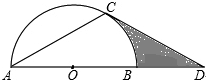 如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.
如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.