题目内容
如图，已知OC、OD是∠AOB内的两条射线，OE平分∠AOC，OF平分∠BOD．
（1）若∠AOB=132°，∠COD=22°，求∠EOF的度数；
（2）若∠EOF=α，∠COD=β，求∠AOB的度数．（用含α、β的代数式表示）
（1）若∠AOB=132°，∠COD=22°，求∠EOF的度数；
（2）若∠EOF=α，∠COD=β，求∠AOB的度数．（用含α、β的代数式表示）
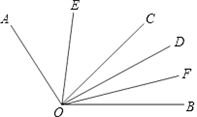
解：（1）依题意，得∠AOC+∠BOD=∠AOB﹣∠COD=110°，
∵OE平分∠AOC，OF平分∠BOD，
∴∠COE+∠DOF=
（∠AOC+∠BOD）=55°，
∴∠EOF=∠COE+∠DOF+∠COD=55°+22°=77°；
（2）依题意，得∠COE+∠DOF=∠EOF﹣∠COD=α﹣β，
∵OE平分∠AOC，OF平分∠BOD，
∴∠AOE+∠BOF=∠COE+∠DOF=α﹣β，
∴∠AOB=∠EOF+∠AOE+∠BOF= α+α﹣β=2α﹣β．
∵OE平分∠AOC，OF平分∠BOD，
∴∠COE+∠DOF=
（∠AOC+∠BOD）=55°，∴∠EOF=∠COE+∠DOF+∠COD=55°+22°=77°；
（2）依题意，得∠COE+∠DOF=∠EOF﹣∠COD=α﹣β，
∵OE平分∠AOC，OF平分∠BOD，
∴∠AOE+∠BOF=∠COE+∠DOF=α﹣β，
∴∠AOB=∠EOF+∠AOE+∠BOF= α+α﹣β=2α﹣β．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
如图，已知OC=OD，还要添加一个条件，才能使△OAD≌△OBC，这个条件是
如图，已知OC、OD是∠AOB内的两条射线，OE平分∠AOC，OF平分∠BOD．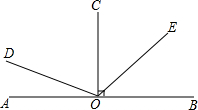
如图，已知OC⊥AB于O，∠AOD：∠COD=1：2．
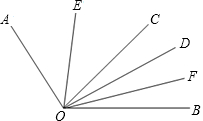如图，已知OC、OD是∠AOB内的两条射线，OE平分∠AOC，OF平分∠BOD．