题目内容
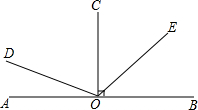 如图,已知OC⊥AB于O,∠AOD:∠COD=1:2.
如图,已知OC⊥AB于O,∠AOD:∠COD=1:2.(1)若OE平分∠BOC,求∠DOE的度数;
(2)若∠AOE的度数比∠COE的度数的3倍多30°,试判断OD与OE的位置关系,并说明理由.
分析:(1)根据垂直的性质,可得∠AOC与∠BOC的度数,根据∠AOD:∠COD=1:2,可得∠COD,根据角平分线的性质,可得∠COE的度数,根据角的和差,可得答案;
(2)根据垂直的性质,可得∠AOC与∠BOC的度数,根据∠AOD:∠COD=1:2,可得∠COD,根据∠AOE的度数比∠COE的度数的3倍多30°,可得∠COE的度数,根据角的和差,可得答案.
(2)根据垂直的性质,可得∠AOC与∠BOC的度数,根据∠AOD:∠COD=1:2,可得∠COD,根据∠AOE的度数比∠COE的度数的3倍多30°,可得∠COE的度数,根据角的和差,可得答案.
解答:解:(1)OC⊥AB于O,
∴∠AOC=∠BOC=90°.
∵∠AOC=90°,∠AOD:∠COD=1:2,
∠DOC=60°.
∵OE平分∠BOC,∠BOC=90°,
∴∠COE=45°,
∠DOE=∠DOC+∠COE=60°+45°
∠DOE=105°;
(2)OD⊥OE,理由如下:
OC⊥AB于O,
∴∠AOC=∠BOC=90°.
∵∠AOC=90°,∠AOD:∠COD=1:2,
∠DOC=60°.
∠AOE-∠COE=2∠COE+30°,
∠AOE-∠COE=90°,
∵2∠COE+30°=90°,
∴∠COE=30°.
∵∠DOE=∠DOC+∠COE=60°+30°=90°,
∴OD⊥OE.
∴∠AOC=∠BOC=90°.
∵∠AOC=90°,∠AOD:∠COD=1:2,
∠DOC=60°.
∵OE平分∠BOC,∠BOC=90°,
∴∠COE=45°,
∠DOE=∠DOC+∠COE=60°+45°
∠DOE=105°;
(2)OD⊥OE,理由如下:
OC⊥AB于O,
∴∠AOC=∠BOC=90°.
∵∠AOC=90°,∠AOD:∠COD=1:2,
∠DOC=60°.
∠AOE-∠COE=2∠COE+30°,
∠AOE-∠COE=90°,
∵2∠COE+30°=90°,
∴∠COE=30°.
∵∠DOE=∠DOC+∠COE=60°+30°=90°,
∴OD⊥OE.
点评:本题考查了垂线,(1)先算出∠DOE,再算出∠COE,根据角的和差得出答案;(2)先算出∠DOE,根据∠AOC=90°,∠AOD:∠COD=1:2,算出∠C0E是解题关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,已知OC⊥AB,OD平分∠AOC,D、O、E三点在同一条直线上,那么∠AOE等于( )
如图,已知OC⊥AB,OD平分∠AOC,D、O、E三点在同一条直线上,那么∠AOE等于( )| A、45° | B、50° | C、135° | D、155° |
 25、如图,已知OC⊥AB,OD⊥OE.
25、如图,已知OC⊥AB,OD⊥OE.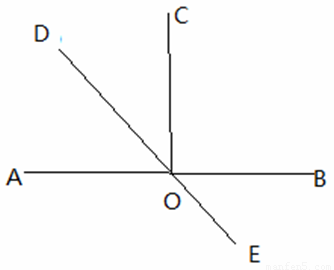
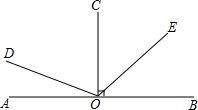 如图,已知OC⊥AB于O,∠AOD:∠COD=1:2.
如图,已知OC⊥AB于O,∠AOD:∠COD=1:2.