题目内容
已知:如图,直线l: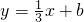 经过点M(0,
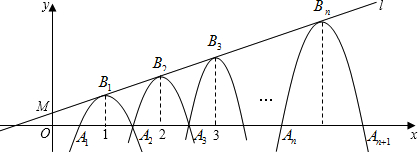
经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),L,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),L,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),L,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),L,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1).
(1)求b的值;
(2)若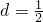 ,求经过点A1、B1、A2的抛物线的解析式;
,求经过点A1、B1、A2的抛物线的解析式;
(3)定义:若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
探究:当d(0<d<1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的d的值.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为 (- ,
, ),对称轴x=-
),对称轴x=- .
.
解:(1)∵M(0, )在y=
)在y= x+b上,
x+b上,
∴ =
= ×0+b
×0+b
∴b= .
.
(2)由(1)得:y= x+
x+ ,
,
∵B1(1,y1)在l上,
∴当x=1时,y1= ×1+
×1+ =
= ,
,
∴B1(1, ).
).
∴设抛物线表达式为:y=a(x-1)2+ (a≠0),
(a≠0),
又∵d= ,
,
∴A1( ,0),
,0),
∴a=- .
.
∴经过点A1、B1、A2的抛物线的解析式为:y=- (x-1)2+
(x-1)2+ .
.
(3)存在美丽抛物线.
由抛物线的对称性可知,所构成的直角三角形必是以抛物线顶点为直角顶点的等腰直角三角形,
∴此等腰直角三角形斜边上的高等于斜边的一半.
又∵0<d<1,
∴等腰直角三角形斜边的长小于2.
∴等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于1.
∵当x=1时,y1= ×1+
×1+ =
= <1,
<1,
当x=2时,y2= ×2+
×2+ =
= <1,
<1,
当x=3时,y3= ×3+
×3+ =1
=1 >1,
>1,
∴美丽抛物线的顶点只有B1、B2.
①若B1为顶点,由B1(1, ),则d=1-
),则d=1- =
= ;
;
②若B2为顶点,由B2(2, ),则d=1-[(2-
),则d=1-[(2- )-1]=
)-1]= ,
,
综上所述,d的值为 或
或 时,存在美丽抛物线.
时,存在美丽抛物线.
分析:(1)由M(0, )在y=
)在y= x+b上,代入即可求得B的值;
x+b上,代入即可求得B的值;
(2)由(1)即可求得:y= x+
x+ ,又由B1(1,y1)在l上,即可求得B1(1,
,又由B1(1,y1)在l上,即可求得B1(1, ),设抛物线表达式为:y=a(x-1)2+
),设抛物线表达式为:y=a(x-1)2+ (a≠0),由d=
(a≠0),由d= ,求得A1(
,求得A1( ,0),即可求得经过点A1、B1、A2的抛物线的解析式;
,0),即可求得经过点A1、B1、A2的抛物线的解析式;
(3)由抛物线的对称性可知,所构成的直角三角形必是以抛物线顶点为直角顶点的等腰直角三角形,由此等腰直角三角形斜边上的高等于斜边的一半.可得等腰直角三角形斜边的长小于2,即可得等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于1,然后分别以x=1,x=2,x=3去分析,即可求得答案.
点评:此题考查了点与函数的关系,待定系数法求函数的解析式,等腰直角三角形的性质等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.
 )在y=
)在y= x+b上,
x+b上,∴
 =
= ×0+b
×0+b∴b=
 .
.(2)由(1)得:y=
 x+
x+ ,
,∵B1(1,y1)在l上,
∴当x=1时,y1=
 ×1+
×1+ =
= ,
,∴B1(1,
 ).
).∴设抛物线表达式为:y=a(x-1)2+
 (a≠0),
(a≠0),又∵d=
 ,
,∴A1(
 ,0),
,0),∴a=-
 .
.∴经过点A1、B1、A2的抛物线的解析式为:y=-
 (x-1)2+
(x-1)2+ .
.(3)存在美丽抛物线.
由抛物线的对称性可知,所构成的直角三角形必是以抛物线顶点为直角顶点的等腰直角三角形,
∴此等腰直角三角形斜边上的高等于斜边的一半.
又∵0<d<1,
∴等腰直角三角形斜边的长小于2.
∴等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于1.
∵当x=1时,y1=
 ×1+
×1+ =
= <1,
<1,当x=2时,y2=
 ×2+
×2+ =
= <1,
<1,当x=3时,y3=
 ×3+
×3+ =1
=1 >1,
>1,∴美丽抛物线的顶点只有B1、B2.
①若B1为顶点,由B1(1,
 ),则d=1-
),则d=1- =
= ;
;②若B2为顶点,由B2(2,
 ),则d=1-[(2-
),则d=1-[(2- )-1]=
)-1]= ,
,综上所述,d的值为
 或
或 时,存在美丽抛物线.
时,存在美丽抛物线.分析:(1)由M(0,
 )在y=
)在y= x+b上,代入即可求得B的值;
x+b上,代入即可求得B的值;(2)由(1)即可求得:y=
 x+
x+ ,又由B1(1,y1)在l上,即可求得B1(1,
,又由B1(1,y1)在l上,即可求得B1(1, ),设抛物线表达式为:y=a(x-1)2+
),设抛物线表达式为:y=a(x-1)2+ (a≠0),由d=
(a≠0),由d= ,求得A1(
,求得A1( ,0),即可求得经过点A1、B1、A2的抛物线的解析式;
,0),即可求得经过点A1、B1、A2的抛物线的解析式;(3)由抛物线的对称性可知,所构成的直角三角形必是以抛物线顶点为直角顶点的等腰直角三角形,由此等腰直角三角形斜边上的高等于斜边的一半.可得等腰直角三角形斜边的长小于2,即可得等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于1,然后分别以x=1,x=2,x=3去分析,即可求得答案.
点评:此题考查了点与函数的关系,待定系数法求函数的解析式,等腰直角三角形的性质等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b经过点A、B.
已知:如图,直线y=kx+b经过点A、B. 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线 已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=
已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=