题目内容
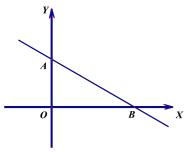
【题目】如图1,已知直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,且
上,且![]() ,若
,若![]() 保持不动,线段
保持不动,线段![]() 向右匀速平移,如图2反映了
向右匀速平移,如图2反映了![]() 的长度
的长度![]() 随时间
随时间![]() 的变化而变化的情况,则:
的变化而变化的情况,则:



(1)在线段![]() 开始平移之前,
开始平移之前,![]()
![]() ;
;
(2)线段![]() 向右平移了
向右平移了 ![]() ,向右平移的速度是
,向右平移的速度是 ![]() ;
;
(3)如图3反映了![]() 的面积
的面积![]() 随时间
随时间![]() 的变化而变化的情况,则
的变化而变化的情况,则
①平行线![]() ,
,![]() 之间的距离是
之间的距离是 ![]() ;
;
②当![]() 时,直接写出
时,直接写出![]() 关于
关于![]() 的函数关系式(不必化简).
的函数关系式(不必化简).
【答案】(1)8;(2)①5;②2;(3)①4;②![]()
【解析】
(1)在线段![]() 开始平移之前,由图2可知,也就是t=0,可得
开始平移之前,由图2可知,也就是t=0,可得![]() .
.
(2)由图2可得,线段![]() 向右平移了
向右平移了![]() ,
,![]() 的长度增加
的长度增加![]() ,由此可求得平移的速度.
,由此可求得平移的速度.
(3)①设平行线![]() ,
,![]() 之间的距离是
之间的距离是![]() ,由图2和图3可知,t=0时,
,由图2和图3可知,t=0时,![]() ,
,![]() 的面积为
的面积为![]() ,由此可求得x.
,由此可求得x.
②由图可知,时间从8s到14s期间,6s时间,![]() 沿直线
沿直线![]() 方向平行移动的距离为
方向平行移动的距离为![]() ,
,
可得平行移动的速度为![]() ,再由面积公式可列出
,再由面积公式可列出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(1)由图象2可知,在线段![]() 开始平移之前,
开始平移之前,![]() ,
,
故答案为:8.
(2)线段![]() 向右平移了
向右平移了![]() ,
,
![]() 的增加长度
的增加长度![]() ,
,
∴向右平移的速度是![]()
故答案为:5;2.
(3)①设平行线![]() ,
,![]() 之间的距离是
之间的距离是![]()
由图2可知,在线段![]() 开始平移之前,
开始平移之前,![]() ,
,
由图3可知,在线段![]() 开始平移之前,
开始平移之前,![]() 的面积为
的面积为![]() .
.
则![]() ,
,
解得,![]() ,
,
故答案为:4.
②由图可知,时间从8s到14s期间,共计6s时间,![]() 沿直线
沿直线![]() 方向平行移动的距离为
方向平行移动的距离为![]()
∴![]() 沿直线
沿直线![]() 方向平行移动的速度为
方向平行移动的速度为![]() ,
,
则![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目