题目内容
4.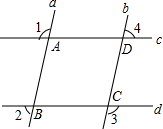 如图,直线c,d与直线a,b相交于点A,B,C,D,∠1=∠3,∠2=∠4.求证:AB=CD.
如图,直线c,d与直线a,b相交于点A,B,C,D,∠1=∠3,∠2=∠4.求证:AB=CD.
分析 根据平行四边形的判定方法易证四边形ABCD是平行四边形,由平行四边形的性质可得AB=CD.
解答 证明:∵∠1=∠DAB,∠3=∠ACB,∠1=∠3,
∴∠DAB=∠ACB,
∵∠2=∠ABC,∠4=∠ADC,∠2=∠4,
∴∠ABC=∠ADC,
∴四边形ABCD是平行四边形,
∴AB=CD.
点评 本题考查了平行四边形的判定和性质,解题的关键是熟记平行四边形的各种判定方法以及善于在图形中挖掘题目隐藏条件:对顶角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.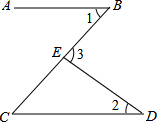 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )| A. | 80° | B. | 70° | C. | 90° | D. | 100° |
19.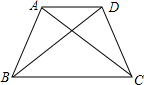 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )| A. | $4\sqrt{2}$ | B. | 4 | C. | $2\sqrt{2}$ | D. | 2 |
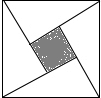 如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是$\frac{1}{9}$,则大、小两个正方形的边长之比是3:1.
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是$\frac{1}{9}$,则大、小两个正方形的边长之比是3:1.