题目内容
20.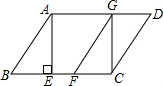 如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.
如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG;
(2)若∠B=60°,当BC=$\frac{3}{2}$AB时,四边形ABFG是菱形;
(3)若∠B=60°,当BC=$\frac{\sqrt{3}+1}{2}$AB时,四边形AECG是正方形.
分析 (1)根据平移的性质,可得:BE=FC,再证明Rt△ABE≌Rt△CDG可得:DG=FC;即可得到BE=DG;
(2)要使四边形ABFG是菱形,须使AB=BF;根据条件找到满足AB=BF时,BC与AB的数量关系即可;
(3)当四边形AECG是正方形时,AE=EC,由AE=$\frac{\sqrt{3}}{2}$AB,可得EC=$\frac{\sqrt{3}}{2}$AB,再有BE=$\frac{1}{2}$AB可得BC=$\frac{\sqrt{3}+1}{2}$AB.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD.
∵AE是BC边上的高,且CG是由AE沿BC方向平移而成,
∴CG⊥AD.AE=CG
∴∠AEB=∠CGD=90°.
∵在Rt△ABE与Rt△CDG中,$\left\{\begin{array}{l}{BE=DG}\\{AB=CD}\end{array}\right.$,
∴Rt△ABE≌Rt△CDG(HL),
∴BE=DG.
(2)解:当BC=$\frac{3}{2}$AB时,四边形ABFG是菱形.
证明:∵AB∥GF,AG∥BF,
∴四边形ABFG是平行四边形.
∵Rt△ABE中,∠B=60°,
∴∠BAE=30°,
∴BE=$\frac{1}{2}$AB(直角三角形中30°所对直角边等于斜边的一半),
∵BE=CF,BC=$\frac{3}{2}$AB,
∴EF=$\frac{1}{2}$AB.
∴AB=BF.
∴四边形ABFG是菱形.
故答案是:$\frac{3}{2}$;
(3)解:BC=$\frac{\sqrt{3}+1}{2}$AB时,四边形AECG是正方形.
∵AE⊥BC,GC⊥CB,
∴AE∥GC,∠AEC=90°,
∵AG∥CE,
∴四边形AECG是矩形,
当AE=EC时,矩形AECG是正方形,
∵∠B=60°,
∴EC=AE=AB•sin60°=$\frac{\sqrt{3}}{2}$AB,BE=$\frac{1}{2}$AB,
∴BC=$\frac{\sqrt{3}+1}{2}$AB.
故答案是:$\frac{\sqrt{3}+1}{2}$.
点评 此题主要考查了平行四边形的性质,正方形的判定,菱形的判定,以及直角三角形的性质.关键是熟练掌握菱形的判定定理,以及平行四边形的性质.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | 6 | B. | 5 | C. | 3 | D. | 2 |
| A. | 2a+3b=5ab | B. | (-1)0=1 | C. | (ab3)2=ab6 | D. | (x+2)2=x2+4 |
 如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )
如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )



 如图,一个直角三角板的直角顶点落右直尺上,若∠1=56°,则∠2的度数为34°.
如图,一个直角三角板的直角顶点落右直尺上,若∠1=56°,则∠2的度数为34°. 如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM.
如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM.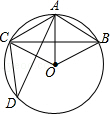 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论:
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论: