题目内容
12．
如图，在?ABCD中，点E，F在对角线BD上，且ED=BF．求证：AE=CF．
分析 根据平行四边形的性质可得AD∥BC，AD=BC，根据平行线的性质可得∠EDA=∠FBC，再加上条件ED=BF可利用SAS判定△AED≌△CFB，进而可得AE=CF．
解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠EDA=∠FBC，
在△AED和△CFB中，$\left\{\begin{array}{l}{AD=BC}\\{∠ADE=∠CBF}\\{BF=DE}\end{array}\right.$，
∴△AED≌△CFB（SAS），
∴AE=CF．
点评 此题主要考查了平行四边形的性质和全等三角形的判定和性质，关键是掌握平行四边形对边平行且相等．
练习册系列答案
相关题目
2．
直线a、b、c、d的位置如图，如果∠1=100°，∠2=100°，∠3=125°，那么∠4等于（ ）
直线a、b、c、d的位置如图，如果∠1=100°，∠2=100°，∠3=125°，那么∠4等于（ ）| A． | 80° | B． | 65° | C． | 60° | D． | 55° |
3．下列运算正确的是（ ）
| A． | x4+x2=x6 | B． | （-2a）3•a=6a4 | ||
| C． | （-x）6÷x2=x3 | D． | a2b•（-2a2b）=-2a4b2 |
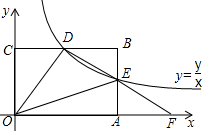如图，点O是平面直角坐标系的原点，反比例函数y=$\frac{k}{x}$位于第一象限的图象经过矩形ABCO边AB的中点E，与边BC交于点D，连接OD，DE，延长DE与x轴交于点F，则△ODF与矩形ABCO的面积比是$\frac{3}{4}$．
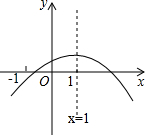已知二次函数y=ax2+bx+c（a≠0）的图象如图，以下结论：
已知，如图，正方形ABCD中，点E，F分别在AD，CD上，且DE=CF，连接BE，AF．