题目内容
【题目】如图,一次函数的图象过![]() 两点.
两点.

(1)求直线![]() 的函数表达式
的函数表达式
(2)直线![]() 交
交![]() 轴于点
轴于点![]() 为直线
为直线![]() 上一动点
上一动点
①求![]() 的最小值;
的最小值;
②![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 为直线
为直线![]() 上另一动点,若
上另一动点,若![]() 是以
是以![]() 为直角边长的等腰直角三角形,求
为直角边长的等腰直角三角形,求![]() 点的坐标.
点的坐标.
【答案】(1)y=-x+3 (2)① ![]() ② D(-1,0) D(
② D(-1,0) D(![]() ,
,![]() )
)
【解析】
(1)代入A,B点的坐标,即可求出解析式;
(2)①由点到直线距离最短为垂线段,根据△ACE为等腰直角三角形求出CE即可
②分类讨论:当DE为斜边时,D点和C重合,根据上问直接写出即可;
当DF为斜边时,D点和C重合,根据上问直接写出即可;
当EF为斜边时,作出△DEF,GN⊥x轴 ED延长线交GN于M,通过△EGD∽△AGC,求出GE的值,根据勾股定理求出GM,即可求出D的纵坐标,代入解析式![]() 得到D的坐标
得到D的坐标
解:(1)设直线![]() 的函数表达式为 y=kx+b
的函数表达式为 y=kx+b
将![]() 代入
代入
得![]() 解得
解得![]()
直线![]() 的函数表达式为 y=-x+3
的函数表达式为 y=-x+3
(2)①如图

作CE⊥AB于E
∵直线![]() 交
交![]() 轴于点C
轴于点C
∴ C(-1,0)
∵![]()
∴△AOB为等腰直角三角形,∠BAO=45°
∴△CEA为等腰直角三角形
∵AC=4
∴CE=![]()
② 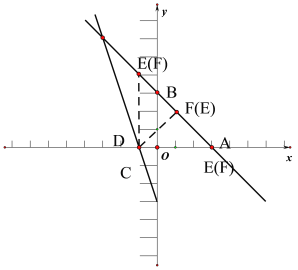
如上图当以DE为斜边时,DF=![]()
∵ CE=![]()
∴ C与D重合
∴D(-1,0)
如上图当以DF为斜边时,DE=![]() 同理
同理
得到D(-1,0)
如图 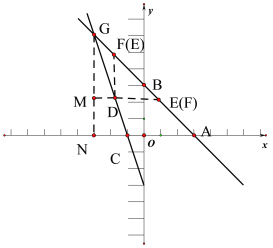
当以EF为斜边时,DE=DF=![]() ∠DEF=∠DFE=45°
∠DEF=∠DFE=45°
根据题意两直线解析式可以求出G(-3,6) 如上图作出△DEF,GN⊥x轴 ED延长线交GN于M 得到GN=6 AG= ∵∠DEF=45° ∠CAB=45° ∴DE∥AC ∵∠AGC是△EGD和△AGC的公共角 ∴△EGD∽△AGC ∴ 解得GE=6 ∵∠DEF=45° ∴GM= ∴MN= ∴D 点的纵坐标为 代入 ∴D( 故答案为:(1)y=-x+3 (2)① ![]()
![]()
![]()
![]()
![]()
![]() 中,解得x=
中,解得x=![]()
![]() ,
,![]() )
)![]() ② D(-1,0) D(
② D(-1,0) D(![]() ,
,![]() )
)

 教材全解字词句篇系列答案
教材全解字词句篇系列答案