��Ŀ����
��֪����ͼ����ABC�У�BC=7����AD=3����B=45�㣬��ֱ��BC�Ķ�ֱ��FM��GN�ֱ��B��C����ͬʱ��������ֱ��AD���ڵ�λ��ƽ�ƣ�ֱ����AD�غ�Ϊֹ������M��NΪ���㣬F��G����ֱ�߷ֱ���AB��AC�Ľ��㣮����ƽ�ƹ�����ʼ�ձ���FG��BC����FM=x����1�����ú�x�Ĵ���ʽ��ʾFG��
��2������E���B����FM����Գƣ���H���C����GN����Գƣ���ƽ�ƹ�����
��xΪ��ֵʱ����E�͵�H�غϣ�
�����E��F��G��HΧ�ɵ��ı��ε����ΪS����H�˶���Bֹͣ����д��S����x
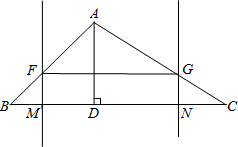 �ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��������1����FC��BGƽ�У�������ֱ��ƽ�еó�����ͬλ����ȣ��������Զ�Ӧ����ȵ������������ƿɵ�������AFG��������ABC���ƣ��������������εĶ�Ӧ��֮�ȵ������Ʊȣ��õ�һ������ʽ������Ӧ��ֵ���뼴����x��ʾ��FG��
��2���ɡ�B=45�㣬AD��BC��ֱ���õ�������ABDΪ����ֱ�������Σ��ɵ�AD=BD=3���Ӷ���BC-BD���CD�������ù��ɶ������AC����������BFMΪ���������Σ���FM=x����ʾ����BE������һ��ֱ����ȣ���һ�Թ����ǣ��õ�������CGN��������CAD���ƣ��������Ƶñ���������Ӧ��ֵ���룬��x��ʾ��CN��������ʾ��CH��
�ٵ�E��H�غ�ʱ����ͼ�εõ�BE+CH=7���ѱ�ʾ����BE��CH�����г�����x�ķ��̣����x��ֵ���ɣ�
�ڷ�����������ǣ�E��BD�Ϻ�E��CD�ϣ��ֱ��ʾ��EH�����������֪�ı���EFGHΪ���Σ�����FG��FM����ʾ����EH���������ε������ʽ���ɱ�ʾ���ı��ε����S���������Ӧ��x�ķ�Χ���ɣ�
��2���ɡ�B=45�㣬AD��BC��ֱ���õ�������ABDΪ����ֱ�������Σ��ɵ�AD=BD=3���Ӷ���BC-BD���CD�������ù��ɶ������AC����������BFMΪ���������Σ���FM=x����ʾ����BE������һ��ֱ����ȣ���һ�Թ����ǣ��õ�������CGN��������CAD���ƣ��������Ƶñ���������Ӧ��ֵ���룬��x��ʾ��CN��������ʾ��CH��
�ٵ�E��H�غ�ʱ����ͼ�εõ�BE+CH=7���ѱ�ʾ����BE��CH�����г�����x�ķ��̣����x��ֵ���ɣ�
�ڷ�����������ǣ�E��BD�Ϻ�E��CD�ϣ��ֱ��ʾ��EH�����������֪�ı���EFGHΪ���Σ�����FG��FM����ʾ����EH���������ε������ʽ���ɱ�ʾ���ı��ε����S���������Ӧ��x�ķ�Χ���ɣ�
��� �⣺��1����FG��BC��
�⣺��1����FG��BC��
���AFG=��ABC����AGF=��ACB��
���AFG�ס�ABC����AD��BC����AD��FG��
��
=
����FM=PD=x��AD=3��BC=7��
��
=
��
��FG=-
x+7����3�֣�
��2���ߡ�B=45�㣬AD��BC��
���ABDΪ����ֱ�������Σ�
��AD=BD=3��CD=BC-BD=4�����ݹ��ɶ����ã�AC=
=5��
�ָ�������ã���BFMΪ����ֱ�������Σ���FM=x��
��BE=2BM=2FM=2x��
�ߡ�GNC=��ADC=90�㣬�ҡ�C=��C��
���CGN�ס�CAD��
��
=
����CD=4��AD=3��GN=FM=x��
��CN=
x��
��CH=2CN=
x��
�ٵ�E��H�غ�ʱ������BE+HC=2x+
x=7�����x=
����4�֣�
�ڵ�E��BD��ʱ����ͼ1��
��EH=7-2x-
x=7-
x��
��S�ı���EFGH=
��FG+EH��•FM=
��-
x+7+7-
x��•x=-
x2+7x��0��x��
������9�֣�
��E��CD��ʱ����ͼ2��
��CE=7-2x��BH=7-
x��
��HE=7-��7-2x��-��7-
x��=
x-7��
��S�ı���EFGH=
��FG+HE��•FM=
��
x-7+7-
x��•x=
x2��
��x��
������12�֣�
 �⣺��1����FG��BC��
�⣺��1����FG��BC�����AFG=��ABC����AGF=��ACB��
���AFG�ס�ABC����AD��BC����AD��FG��
��
| FG |
| BC |
| AP |
| AD |
��
| FG |
| 7 |
| 3-x |
| 3 |
��FG=-
| 7 |
| 3 |
��2���ߡ�B=45�㣬AD��BC��
���ABDΪ����ֱ�������Σ�
��AD=BD=3��CD=BC-BD=4�����ݹ��ɶ����ã�AC=
| AD2+CD2 |
�ָ�������ã���BFMΪ����ֱ�������Σ���FM=x��
��BE=2BM=2FM=2x��
�ߡ�GNC=��ADC=90�㣬�ҡ�C=��C��
���CGN�ס�CAD��
��
| CN |
| CD |
| GN |
| AD |
��CN=
| 4 |
| 3 |
��CH=2CN=
| 8 |
| 3 |

�ٵ�E��H�غ�ʱ������BE+HC=2x+
| 8 |
| 3 |
| 3 |
| 2 |
�ڵ�E��BD��ʱ����ͼ1��
��EH=7-2x-
| 8 |
| 3 |
| 14 |
| 3 |
��S�ı���EFGH=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 3 |
| 14 |
| 3 |
| 7 |
| 2 |
| 3 |
| 2 |
��E��CD��ʱ����ͼ2��
��CE=7-2x��BH=7-
| 8 |
| 3 |
��HE=7-��7-2x��-��7-
| 8 |
| 3 |
| 14 |
| 3 |
��S�ı���EFGH=
| 1 |
| 2 |
| 1 |
| 2 |
| 14 |
| 3 |
| 7 |
| 3 |
| 7 |
| 6 |
| 3 |
| 2 |
| 21 |
| 8 |
���������⿼���������������ж������ʣ�����ֱ�������ε����ʣ��ԳƵ����ʣ��Լ����ε������ʽ������һ����������������ͬʱ������ۺ����⣬���ڸ���������̽�������ƣ����������Ƶ�����������⣬�������������к�����ϵʽ�������������������εĵ������еĹ�ϵ������Ҫ����֪������̽���ϵ��µ���x�Ĺ�ϵ��Ϊ�������Ĺؼ�������ʱ�������п����ȵ����ͣ���˽����������ʱ��Ӧע���ھ����е�����������ע�����ν�ϡ���ѧ��ģ���������۵���ѧ˼������ã�

��ϰ��ϵ�д�
�����Ŀ
 17����֪����ͼ����ABC�У���BAC=90�㣬AD��BC�ڵ�D��BEƽ�֡�ABC����AD�ڵ�M��ANƽ�֡�DAC����BC�ڵ�N��
17����֪����ͼ����ABC�У���BAC=90�㣬AD��BC�ڵ�D��BEƽ�֡�ABC����AD�ڵ�M��ANƽ�֡�DAC����BC�ڵ�N�� ��֪����ͼ����ABC����ACB ��ƽ�����ཻ�ڵ�F����F��DE��BC��D����AC ��E����AB=6��AC=5����������ADE���ܳ���
��֪����ͼ����ABC����ACB ��ƽ�����ཻ�ڵ�F����F��DE��BC��D����AC ��E����AB=6��AC=5����������ADE���ܳ��� ��֪����ͼ����ABC�ǵȱ������Σ���D��AB�ϣ���E��AC���ӳ����ϣ���BD=CE��DE��BC��F����֤��BF=CF+CE��
��֪����ͼ����ABC�ǵȱ������Σ���D��AB�ϣ���E��AC���ӳ����ϣ���BD=CE��DE��BC��F����֤��BF=CF+CE�� ��֪����ͼ����ABC�У�AB=AC=10��BC=16����D��BC�ϣ�DA��CA��A��
��֪����ͼ����ABC�У�AB=AC=10��BC=16����D��BC�ϣ�DA��CA��A�� ��֪����ͼ����ABC�У�AD��BC��BD=DE����E��AC�Ĵ�ֱƽ�����ϣ�
��֪����ͼ����ABC�У�AD��BC��BD=DE����E��AC�Ĵ�ֱƽ�����ϣ�