题目内容
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2= ![]() GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2 ![]() 时,BE的长为
时,BE的长为 ![]()
![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( ) 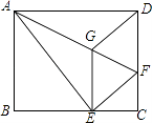
A.1
B.2
C.3
D.4
【答案】D
【解析】解:∵GE∥DF, ∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.故①正确;
∴DG=GE=DF=EF.
∴四边形EFDG为菱形,故②正确;
如图1所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF= ![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴ ![]() =
= ![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO= ![]() GF,DF=EG,
GF,DF=EG,
∴EG2= ![]() GFAF.故③正确;
GFAF.故③正确;
如图2所示:过点G作GH⊥DC,垂足为H.
∵EG2= ![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2 ![]() ,
,
∴20= ![]() FG(FG+6),整理得:FG2+6FG﹣40=0.
FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2 ![]() ,AF=10,
,AF=10,
∴AD= ![]() =4
=4 ![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴GH= ![]() ,
,
∴BE=AD﹣GH=4 ![]() ﹣
﹣ ![]() =
= ![]() .故④正确.
.故④正确.
故选D.
先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF,连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF= ![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系,过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系,过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案





