题目内容
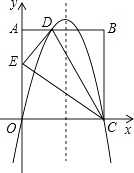
【题目】平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别是为（0,3）、（-1,0），将此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′.
（1）若抛物线过点C、A、A′，求此抛物线的解析式；
（2）求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长；
（3）点M是第一象限内抛物线上的一动点，问：点M在何处时；△AMA′的面积最大？最大面积是多少？并求出此时点M的坐标.
【答案】
（1）
解：∵□A′B′OC′由□ABOC旋转得到，且点A的坐标为（0,3）,
点A′的坐标为（3,0）.
∴抛物线过点C（-1,0），A（0,3），A′（3,0），
设抛物线的解析式为y=ax2+bx+c(a≠0)，可得
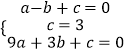解得 
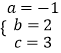
∴过点C，A，A′的抛物线的解析式为y=-x2+2x+3.
（2）
解：∵AB//CO，∴∠OAB=∠AOC=90°，
∴OB= 
，
又∠OC′D=∠OCA=∠B，
∠C′OD=∠BOA，∴△C′OD~△BOA，
又OC′=OC=1,
∴ 
，
又△ABO的周长为4+ 
，
∴△C′OD的周长为 
.
（3）
解：连接OM，设M点的坐标为（m，n），
∵点M在抛物线上，
∴n=-m2+2m+3，
∴ 
，
= 
OA·m+ OA′·n- OA·OA′
= 
（m+n）- 
= (m+n-3)
= 
(m2-3m)= （m ）2+ 
.
∵0<m<3，∴当m= 时，n= 
，△AMA′的面积有最大值，
∴当点M的坐标为（ ， ）时，△AMA′的面积有最大值，且最大值为 .
【解析】（1）需要求A′的坐标，由A（0,3）绕点O顺时针旋转90°，则A′在x轴上且OA′=OA=3，则A′(3,0)；运用待定系数法求抛物线的解析式；（2）根据勾股定理易求得OB的长；由角OC′D=角OCA=角B，角C′OD=角BOA，则△C′OD~△BOA，根据相似三角形的周长比等于相似比，可先求得相似比和△BOA的周长，则可求出△OC′D的周长；（3）可设M（m，n）代入抛物线可得n与m的关系式，而 ，由面积= 底乘高，将上式进行化简，可得 
与m的关系式，由0<m<3，讨论m取何值时 最大.
