题目内容
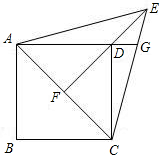 如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连接ED并延长交AC于点F.
如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连接ED并延长交AC于点F.(Ⅰ)求证:EF⊥AC;
(Ⅱ)延长AD交CE于点G,试确定线段DG和线段DE的数量关系.
分析:(1)可由SSS证得△AED≌△CED,得到∠AED=∠CED,根据等腰三角形的性质:顶角的平分线与底边上的高重合知,EF⊥AC;
(2)过G作GM⊥EF,垂足为M,则可证得△DMG为等腰直角三角形,△MGE为含30度角的直角三角形,进而设出参数,解△DMG和,△MGE这两个直角三角形,求得DG与DE的比.
(2)过G作GM⊥EF,垂足为M,则可证得△DMG为等腰直角三角形,△MGE为含30度角的直角三角形,进而设出参数,解△DMG和,△MGE这两个直角三角形,求得DG与DE的比.
解答:(1)证明:由已知,得
,
∴△AED≌△CED,(2分)
∴∠AED=∠CED,(3分)
又∵△AEC为等边三角形,
∴EF⊥AC;(4分)
(2)解法一: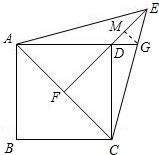
过G作GM⊥EF,垂足为M,(5分)
由已知和(Ⅰ),得
∠AED=∠CED=30°,∠EAD=15°
∴∠EDG=45°,
∴MD=GM(6分)
设GM=x,则DG=
x
在Rt△MEG中,EG=2MG=2x,(7分)
∴EM=
x(8分)
∴ED=
x+x=(
+1)x(9分)
∴
=
=
即DE=
DG(或DG=
DE)(10分)
解法二: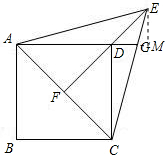
过E作EM⊥AD,垂足为M
在Rt△MDE中,
∵∠EDM=∠MED=45°,
∴EM=DM
设EM=DM=x,
则DE=
x(6分)
在Rt△AEF中,cot30°=
,
∴DF=AF=
(7分)
∴AD=
•
=(
+1)x(8分)
∵△CDG∽△AME,
∴
=
即
=
∴DG=(
-1)x(9分)
∴
=
=
即DE=
DG(或DG=
DE).(10分)
|
∴△AED≌△CED,(2分)
∴∠AED=∠CED,(3分)
又∵△AEC为等边三角形,
∴EF⊥AC;(4分)
(2)解法一:

过G作GM⊥EF,垂足为M,(5分)
由已知和(Ⅰ),得
∠AED=∠CED=30°,∠EAD=15°
∴∠EDG=45°,
∴MD=GM(6分)
设GM=x,则DG=
| 2 |
在Rt△MEG中,EG=2MG=2x,(7分)
∴EM=
| 3 |
∴ED=
| 3 |
| 3 |
∴
| ED |
| DG |
(
| ||
|
| ||||
| 2 |
即DE=
| ||||
| 2 |
| ||||
| 2 |
解法二:

过E作EM⊥AD,垂足为M
在Rt△MDE中,
∵∠EDM=∠MED=45°,
∴EM=DM
设EM=DM=x,
则DE=
| 2 |
在Rt△AEF中,cot30°=
| DE+DF |
| AF |
∴DF=AF=
(
| ||||
| 2 |
∴AD=
(
| ||||
| 2 |
| 2 |
=(
| 3 |
∵△CDG∽△AME,
∴
| DG |
| EM |
| CD |
| AM |
即
| DG |
| x |
(
| ||
(
|
∴DG=(
| 3 |
∴
| DE |
| DG |
| ||
(
|
| ||||
| 2 |
即DE=
| ||||
| 2 |
| ||||
| 2 |
点评:本题利用了等边三角形和等腰直角三角形的性质,直角三角形的性质,锐角三角函数的概念求解.

练习册系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6