题目内容
己知关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根是1,且a,b满足b= ,求这个一元二次方程的另一根.
,求这个一元二次方程的另一根.
解:∵ ,
,
∴a=2,
∴b=-3,
∴原方程为2x2-3x+c=0,
设方程另一个根为t,
∴1+t=-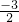 ,
,
∴t= ,
,
即这个一元二次方程的另一根为 .
.
分析:根据二次根式有意义的条件可求出a=2,则b=-3,原方程为2x2-3x+c=0,设方程另一个根为t,根据根与系数的关系得到1+t=-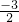 ,然后解一次方程即可.
,然后解一次方程即可.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .也考查了二次根式有意义的条件.
.也考查了二次根式有意义的条件.
 ,
,∴a=2,
∴b=-3,
∴原方程为2x2-3x+c=0,
设方程另一个根为t,
∴1+t=-
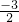 ,
,∴t=
 ,
,即这个一元二次方程的另一根为
 .
.分析:根据二次根式有意义的条件可求出a=2,则b=-3,原方程为2x2-3x+c=0,设方程另一个根为t,根据根与系数的关系得到1+t=-
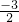 ,然后解一次方程即可.
,然后解一次方程即可.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .也考查了二次根式有意义的条件.
.也考查了二次根式有意义的条件. 
练习册系列答案
相关题目
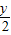 .
.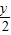 代入已知方程,得(
代入已知方程,得(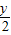 )2+
)2+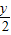 -1=0
-1=0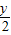 .
. 代入已知方程,得(
代入已知方程,得( )2+
)2+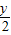 -1=0
-1=0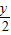 .
.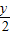 代入已知方程,得(
代入已知方程,得(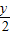 )2+
)2+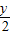 -1=0
-1=0